题目

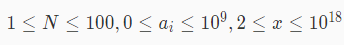
题解

等比数列,最后统一除以(x-1)(这里数据都存在逆元。。。。)
(不存在逆元可以考虑表示成:x*p^y的pair形式,最后上下把p的次数相减(类似扩展Lucas)
具体操作:(a,b)*(c,d)=(a*c,b+d)
然后检查(a,b):如果a%mod==0,(a,b)->(a/mod,b+1),否则(a,b)->(a%mod,b)
显然这样取模,mod的次数不会减少。
)
求:lcm(x^(ai+1)-1)
令f(a)=x^(a+1)-1
一看,根本无法直接做
上一个这样lcm的是:51nod斐波那契最小公倍数,gcd(f[a],f[b])=f[gcd(a,b)]
利用gcd和lcm的容斥关系!
这个是否也可以?
不妨考虑gcd(f(a),f(b))
发现,利用辗转相减可以证明:gcd(f(a),f(b))=gcd(f(b),f(a-b))=f(gcd(a,b))
但是要考虑所有的集合。。。
结论:gcd不会太多
开个map,暴力遍历枚举
每个map[i].fi存gcd,map[i].se存这个gcd贡献的指数次数(上-下)
拼凑ai新加的gcd把原来贡献取反加入即可。
最后++map[a[i]]
#include<bits/stdc++.h> #define reg register int #define il inline #define fi first #define se second #define mk(a,b) make_pair(a,b) #define numb (ch^'0') #define pb push_back #define solid const auto & #define enter cout<<endl using namespace std; typedef long long ll; template<class T>il void rd(T &x){char ch;x=0;bool fl=false;while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);for(x=numb;isdigit(ch=getchar());x=x*10+numb);(fl==true)&&(x=-x); } template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');} template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');} template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');}namespace Miracle{ const int N=105; const int mod=1e9+7; ll x,n; ll a[N]; int qm(int x,int y){int ret=1;while(y){if(y&1) ret=(ll)ret*x%mod;x=(ll)x*x%mod;y>>=1;}return ret; } unordered_map<int,int>mp,t; int gcd(int a,int b){return b?gcd(b,a%b):a; } int main(){rd(x);rd(n);x%=mod;for(reg i=1;i<=n;++i) rd(a[i]),++a[i];for(reg i=1;i<=n;++i){t=mp;for(solid j:mp){int g=gcd(j.fi,a[i]);t[g]+=-j.se;}t[a[i]]++;mp.swap(t);}ll ans=1;for(solid j:mp){if(j.se>=0) ans=ans*qm((qm(x,j.fi)+mod-1)%mod,j.se)%mod;else ans=ans*qm(qm((qm(x,j.fi)+mod-1)%mod,-j.se),mod-2)%mod;}ans=(ll)ans*qm((x+mod-1)%mod,mod-2)%mod;ot(ans);return 0; }} signed main(){Miracle::main();return 0; }/*Author: *Miracle* */
min-max容斥吼啊
结论吼啊
暴力吼啊
