建设拍卖网站google安卓版下载

通过前两次的内容(如何理解二次型的定义),我们知道学习二次型的最佳办法是将其理解为一个二次方程,并研究如何将所有的二次方程图像进行分类。在上一讲中(如何理解二次型的线性替换),我们已经知道了研究二次型的最主要的工具:非退化的线性替换。说白了,就是换一下坐标系而已。
那到底该如何选择坐标系,才能确定二次方程的大致的图像呢(注意这里是大致的图像!!!)? 带着这个问题,下面为大家简单介绍一下实二次型的标准型和惯性定理。先来看看剧情介绍吧:
- 为什么需要标准形
- 标准方程在直角坐标系下的图像
- 标准方程在一般坐标系下的图像
- 惯性定理的几何解释
- 从线性变换的角度理解惯性定理
为什么需要标准型?
我们就简单将一个只含有平方项的二次型称为标准形吧,别忘记了
- 系统研究二次型的最初的目的就是考虑二次方程的图像分类。而线性替换的实质是:方程图像不变,改变的仅仅是坐标系和图像的表达式。
- 任何一个二次型都能经过坐标系的选择(非退化的线性替换)化为标准形。
记住了这两点,为什么需要标准型的问题就很简单了:
- 首先,一个标准的二次方程的图像是容易知道的;
- 其次,利用非退化的线性替换可以将一个未知图像的放到一个坐标系(线性替换矩阵)中,使得图像的方程变成标准形;
- 最后,利用这个方程的标准形的图像便可以得到了原方程的图像。
如下图所示:

可是,如何确定一个标准方程在非直角坐标系下的图像呢?例如
标准的二次方程在直角坐标系下的图像
如果坐标系是一个直角坐标系,相信大家都知道标准方程的图像:


标准的二次方程在一般坐标系下的图像
如果非退化的线性替换选取的不是一个直角坐标系,这时候如何知道一个标准二次方程得图像呢?
- 对于一个实二次型来说,总是可以找到一个直角坐标系使得方程变为一个标准方程的。因为一个实对称矩阵总是可以被正交对角化,这就是所谓的二次型的正交替换法(敬请期待后期推送)。
- 哪怕不是直角坐标系,这个坐标系中的标准方程也是简单的。
例如:下面为
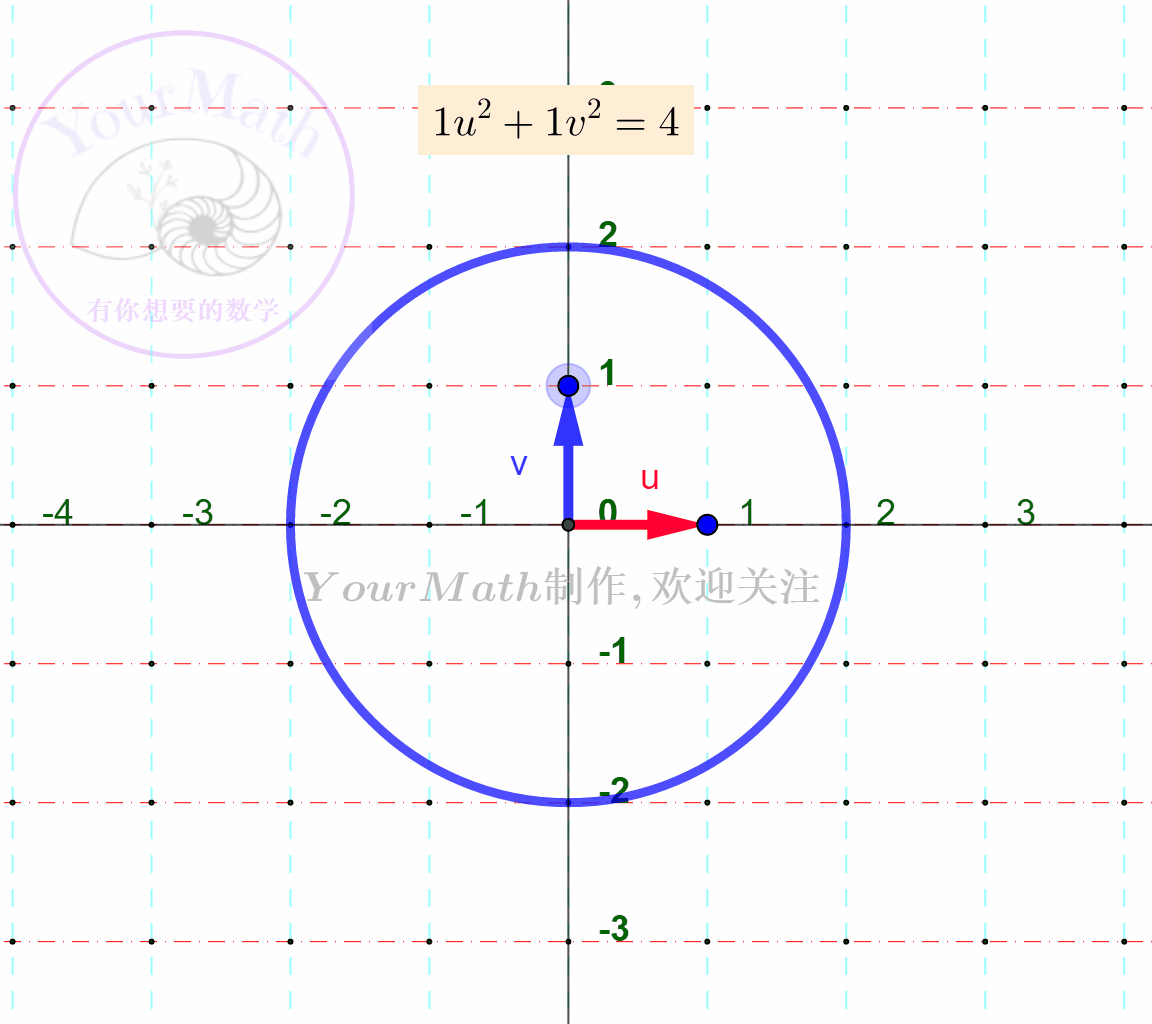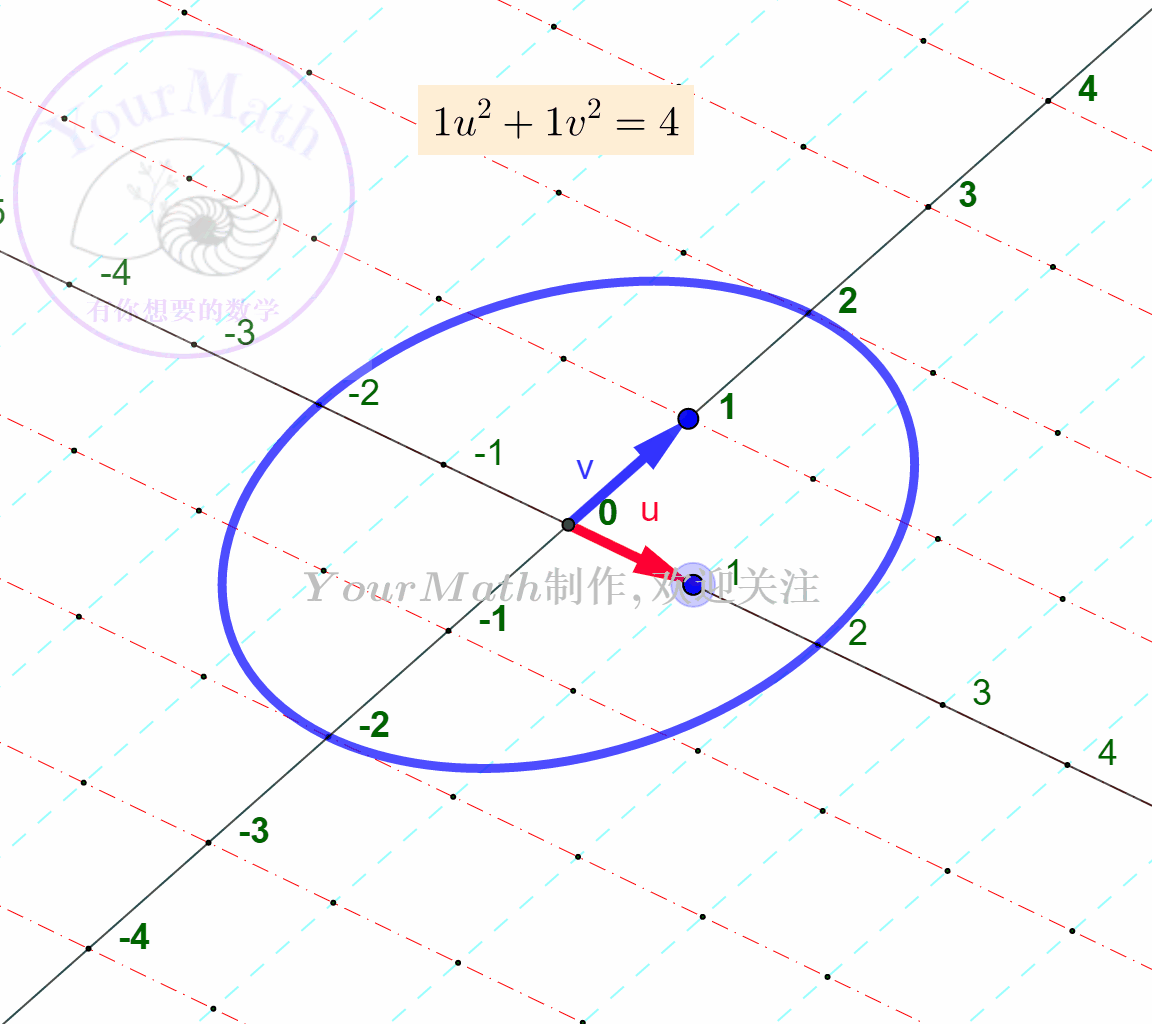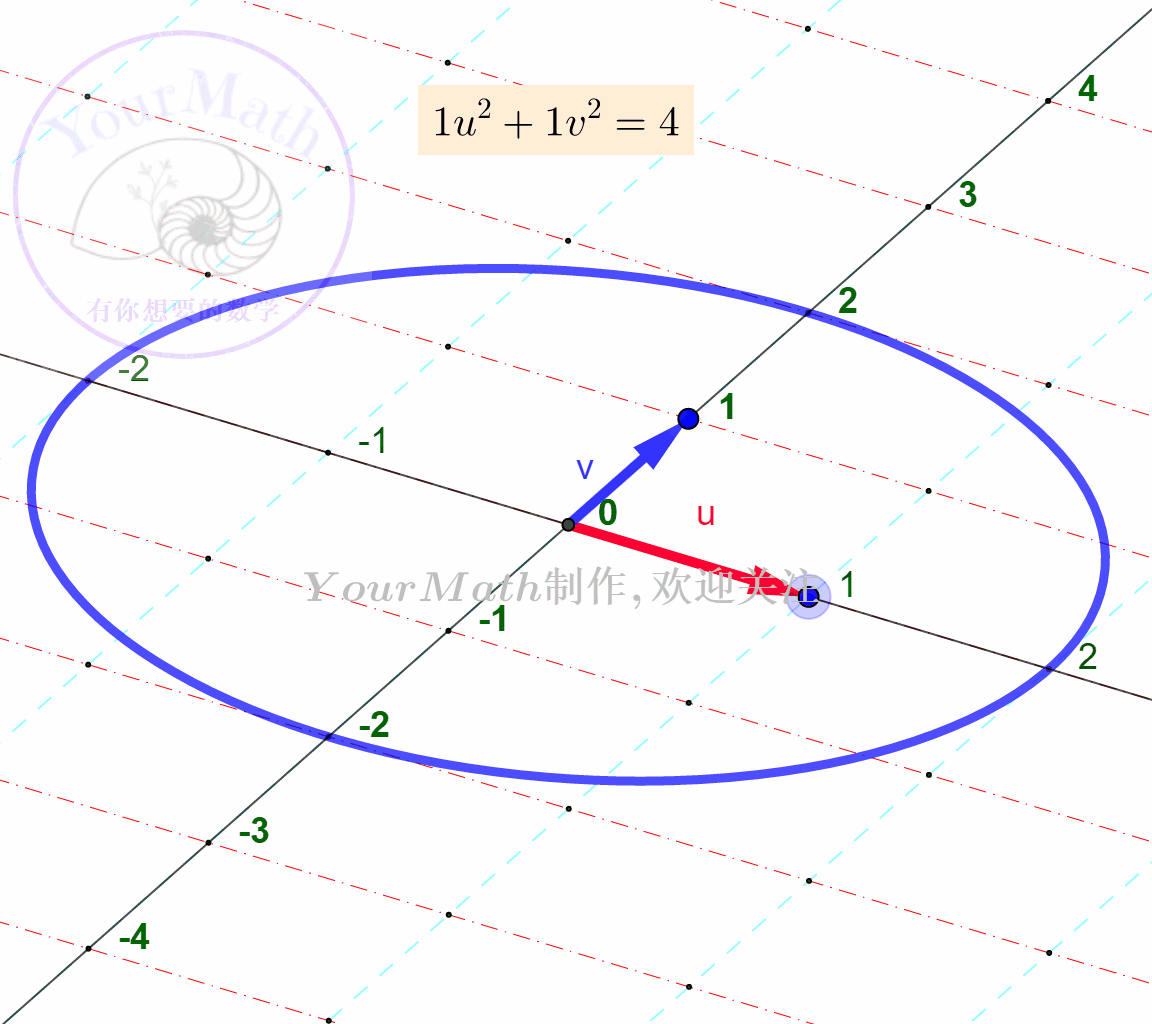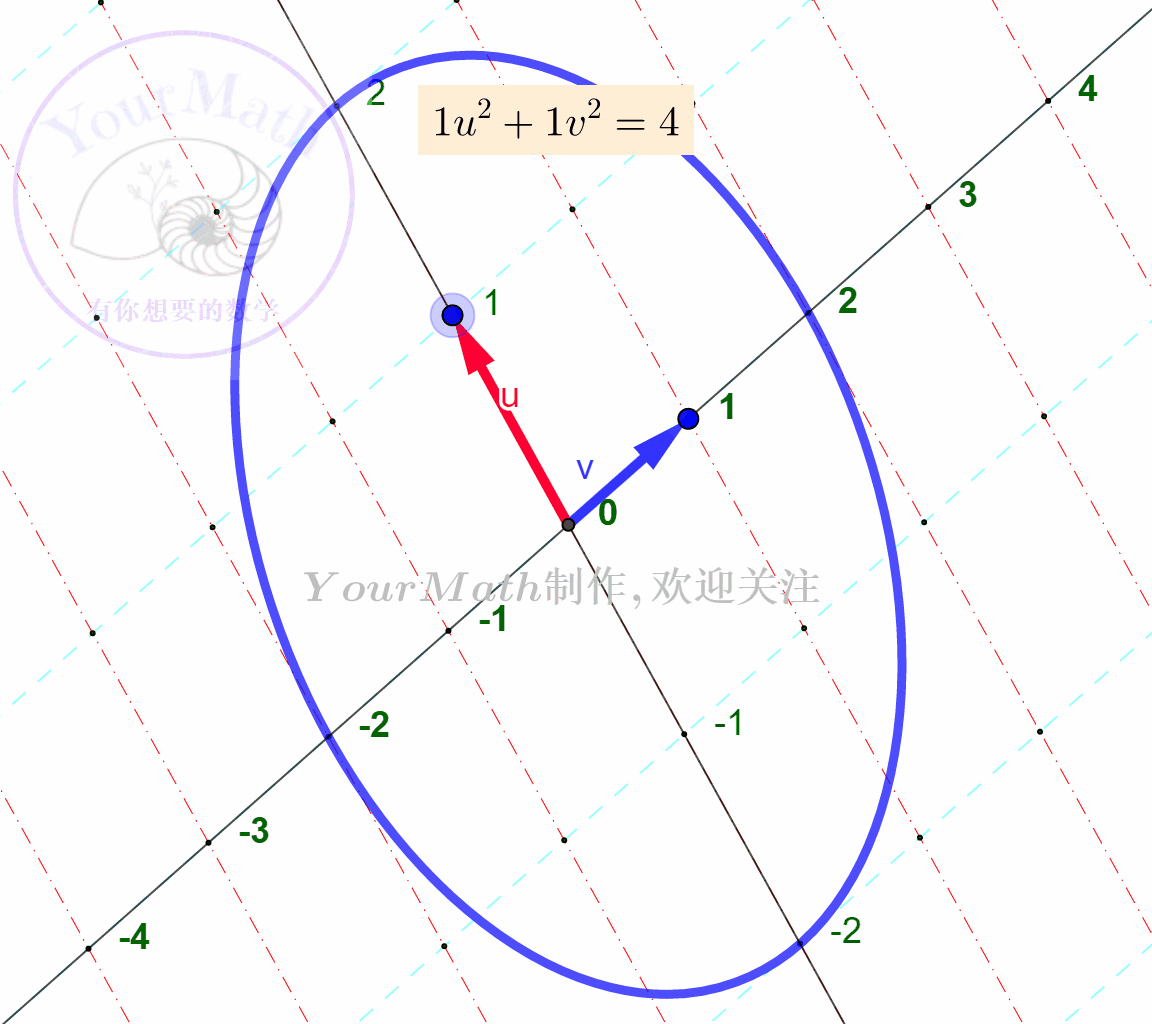
下面为
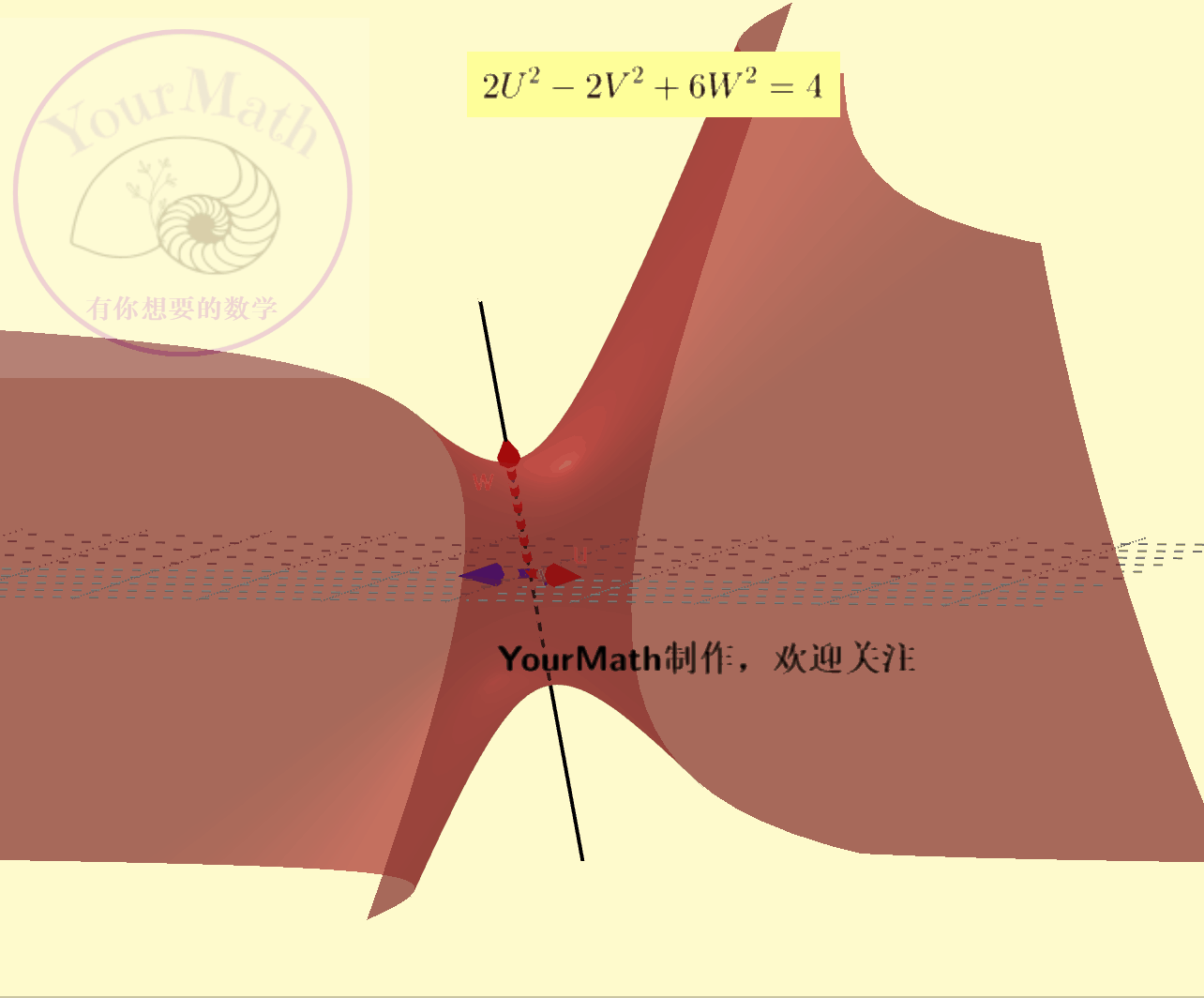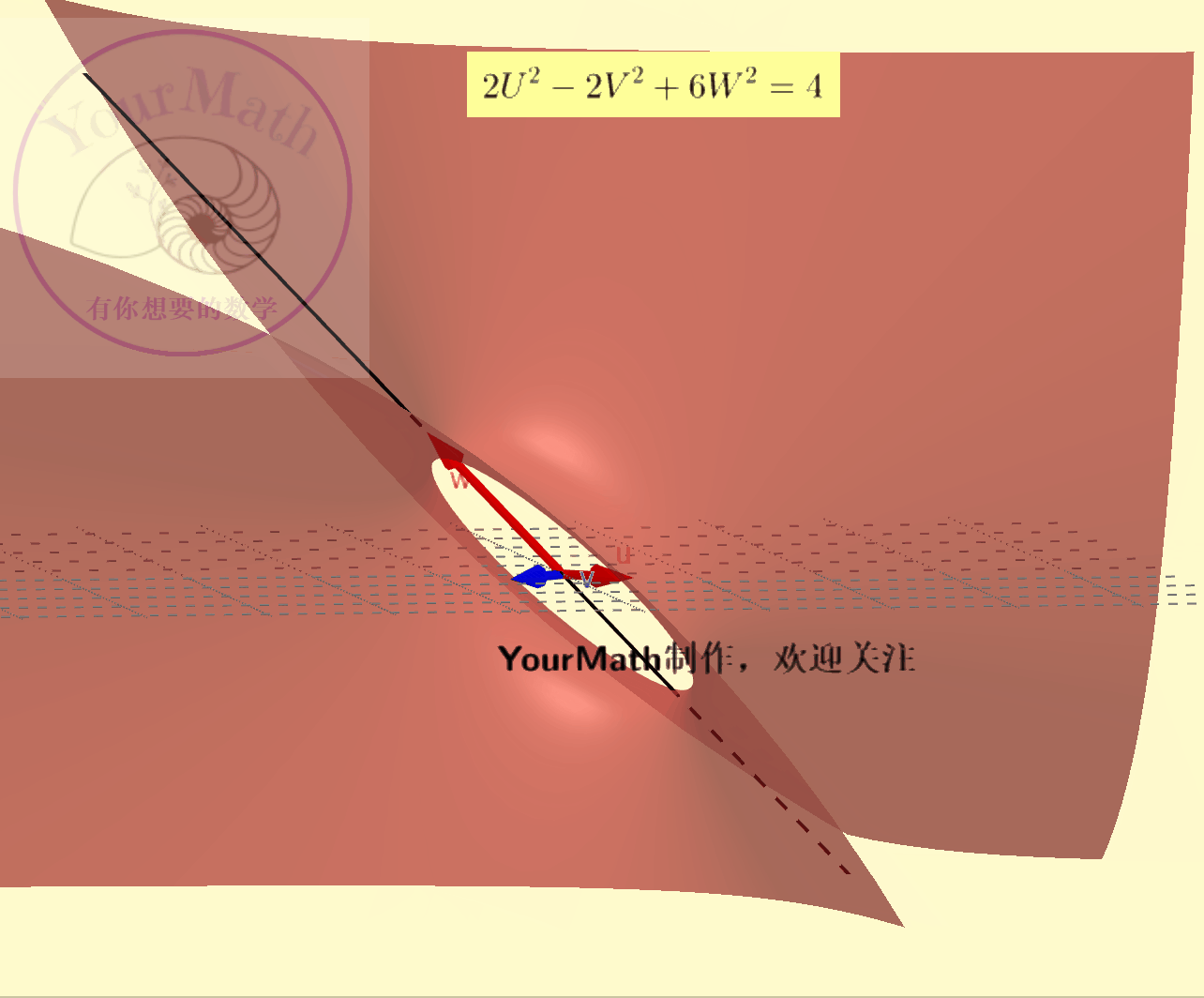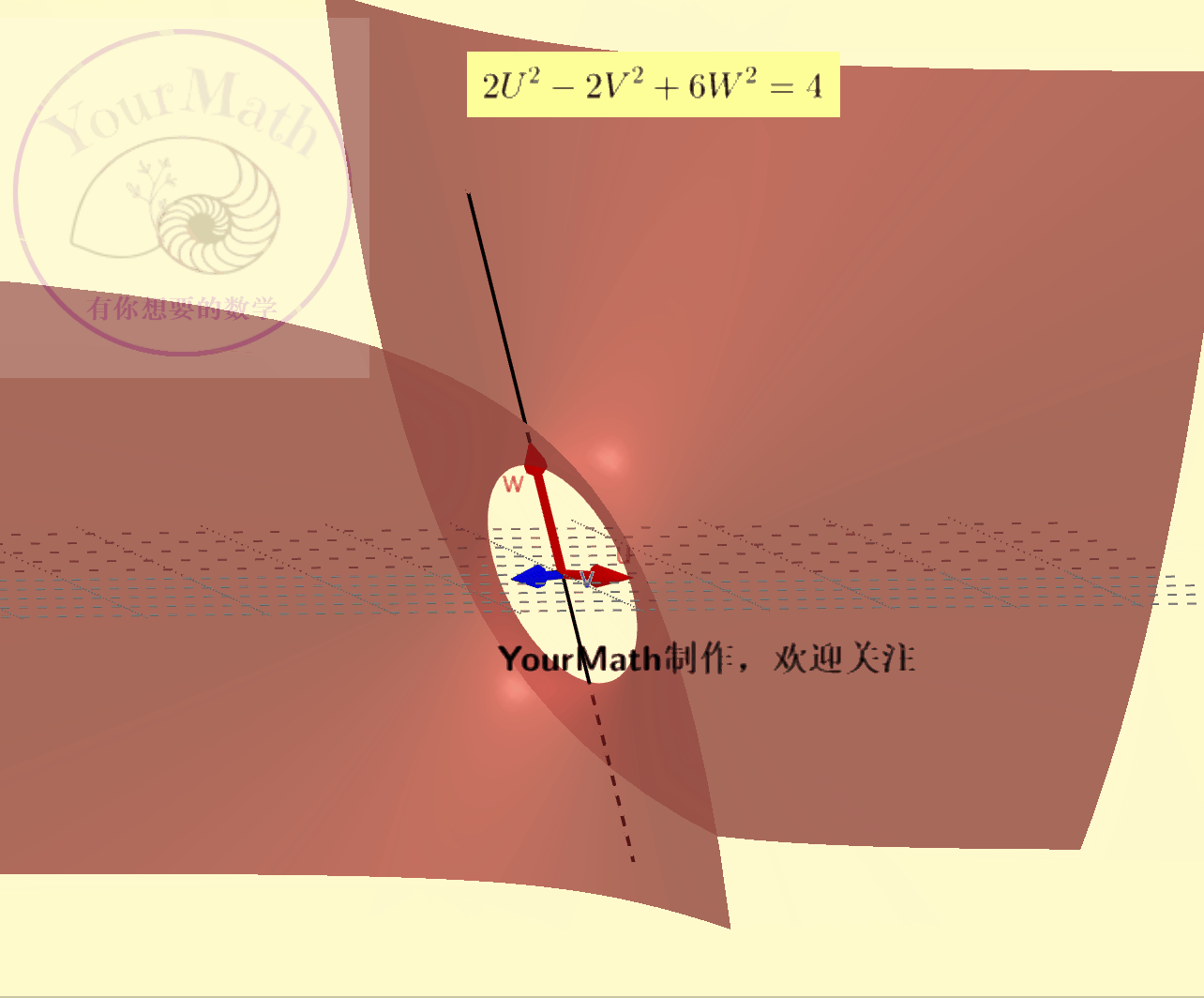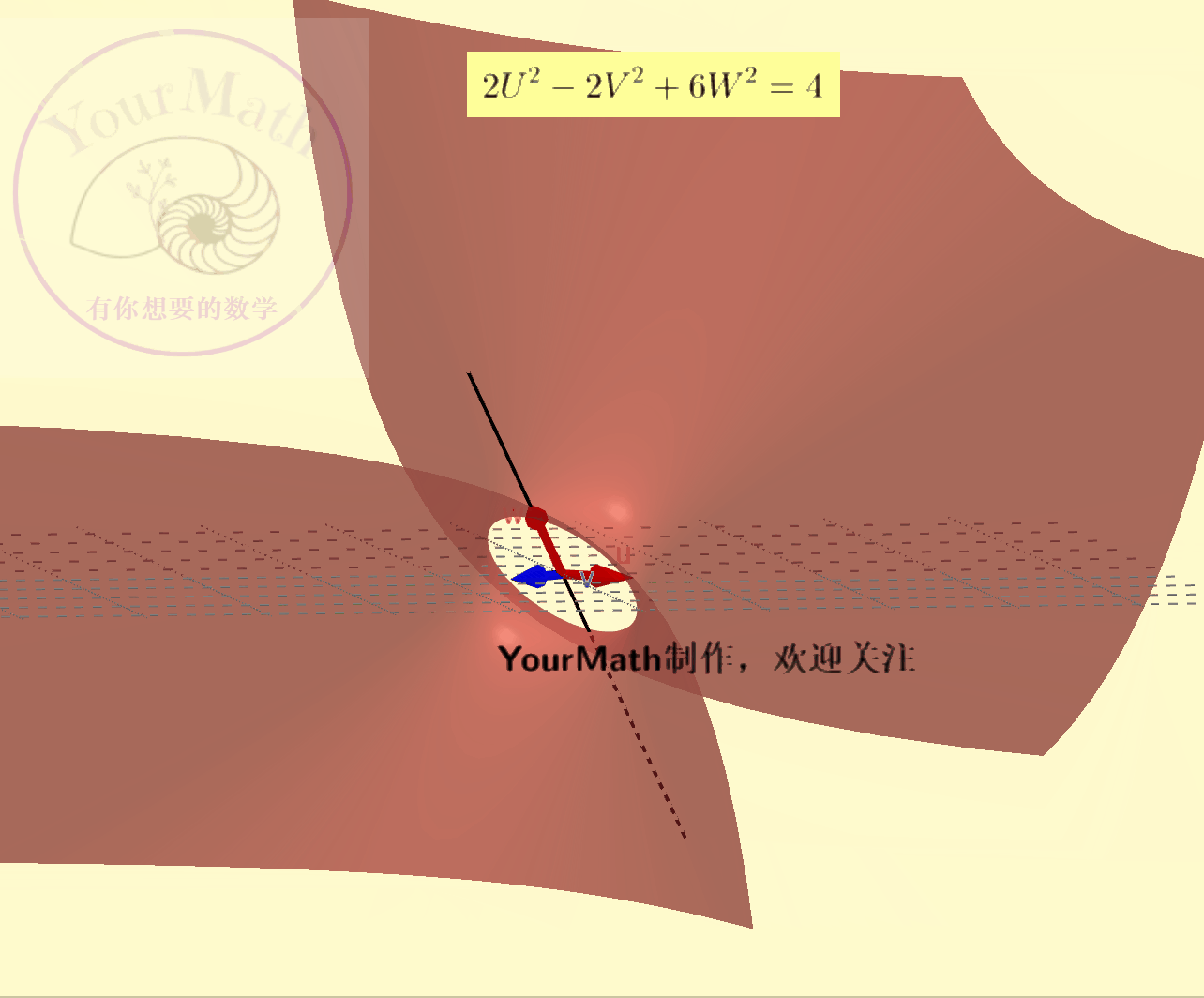
如果把圆理解为长轴=短轴的椭圆,球面理解为特殊的椭球面。实际上
- 椭圆的方程在任何
坐标系下均为
其中
- 椭球面的方程在任何
坐标系下均为
其中
- 其它标准形的情况与直角坐标系下是类似的
如果仅仅为了解一个二次方程的大致图像(注意是大致图像哦),每一个坐标系下的标准形都是可以做到的。那么,如何确定一个方程的精确图像呢?例如求椭圆的长短轴的大小,某一个球面的体积。例如: 已知椭圆曲线方程
如何求这个椭圆的长轴与短轴呢?这就需要特殊的线性替换(二次型的正交替换了)。敬请期待后期推送
从几何角度理解惯性定理
二次型的惯性定理归功于Sylvester,起源于力学。可以表述为: 有限的实二次型的规范形是唯一的。 也就是说,不论选取怎样的坐标变换使它化为仅含平方项的标准形,其正、负惯性指数与所选取的坐标变换无关。 注:二次型的标准形不是唯一的,它与所选的坐标变换有关,惯性定理告诉我们二次型的正负惯性指数是唯一不变的,它反映了二次型的本质特征。
例如,我们取了平面上一个中心在原点的一个椭圆
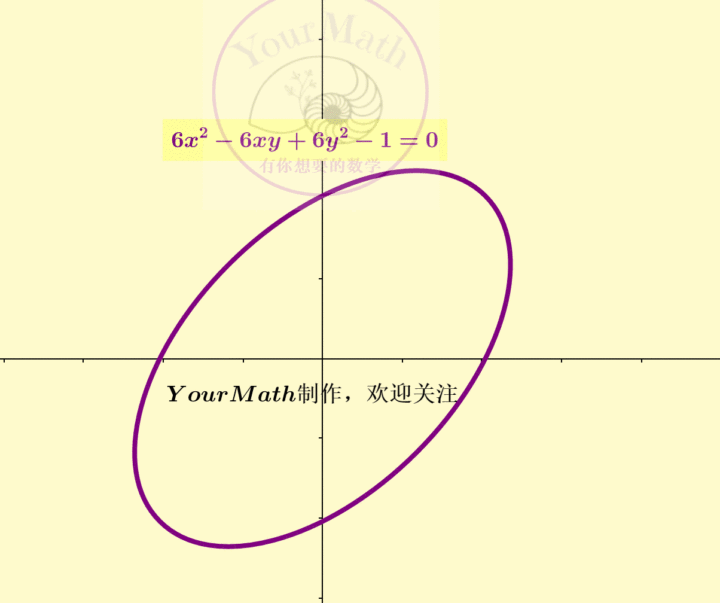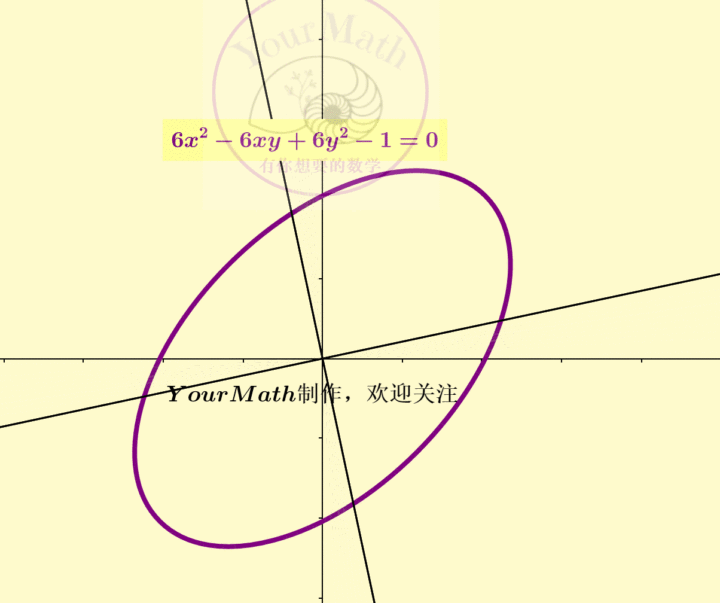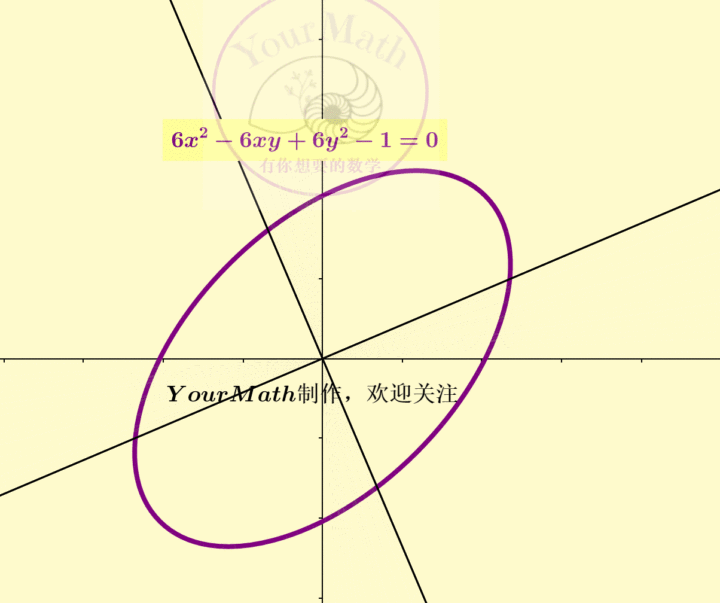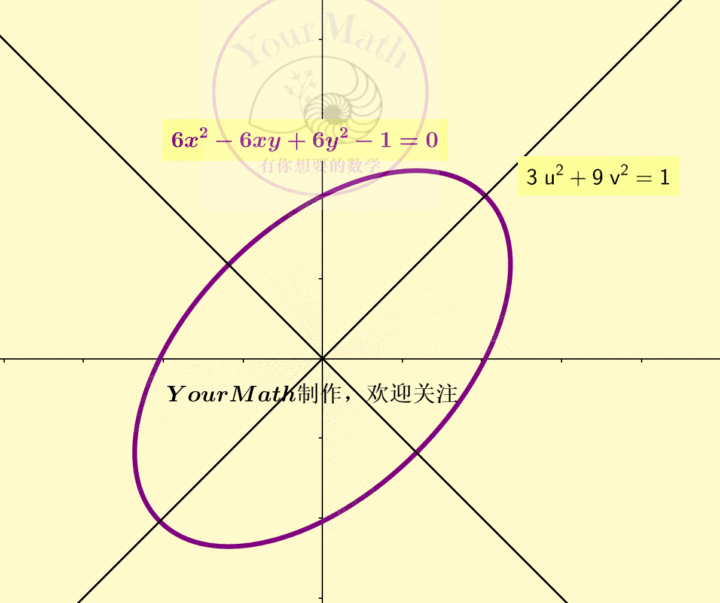
从而这个椭圆的规范形为
注意二次型的标准形不是唯一的,它与所选的坐标变换有关。由之前介绍的标准二次方程在一般坐标系下的图像可知,不论选取哪一个
也就说,一个椭圆的规范形是唯一的。
从线性变换角度理解惯性定理
因为坐标系的替换也可以理解为一个线性变换。因此,每一个线性替换可以理解为将原来的二次曲线,通过线性替换矩阵所对应的线性变换,变为了一个新的二次曲线。下图为一个椭圆经过不同的线性变换后的图像:
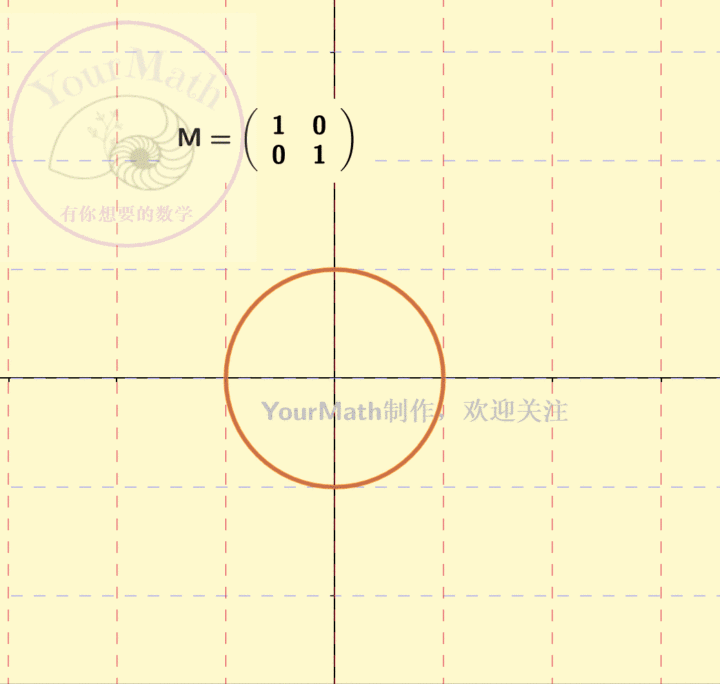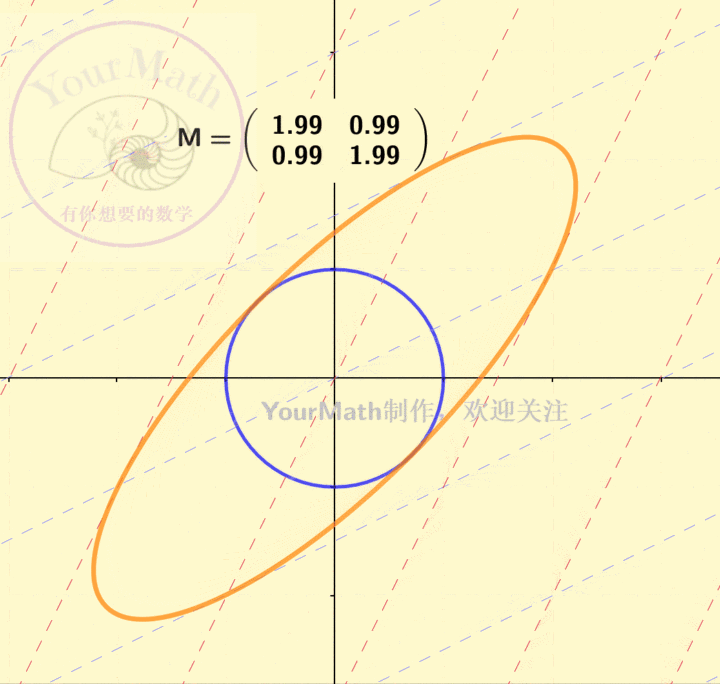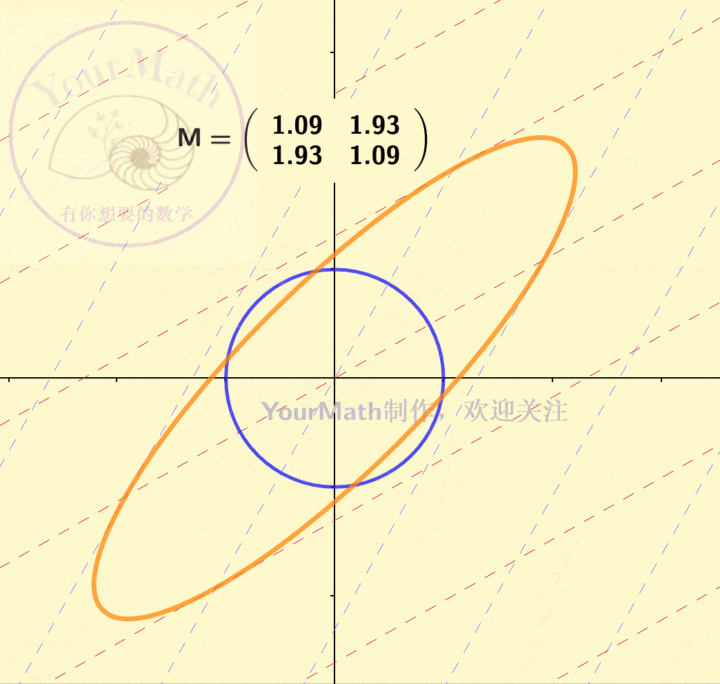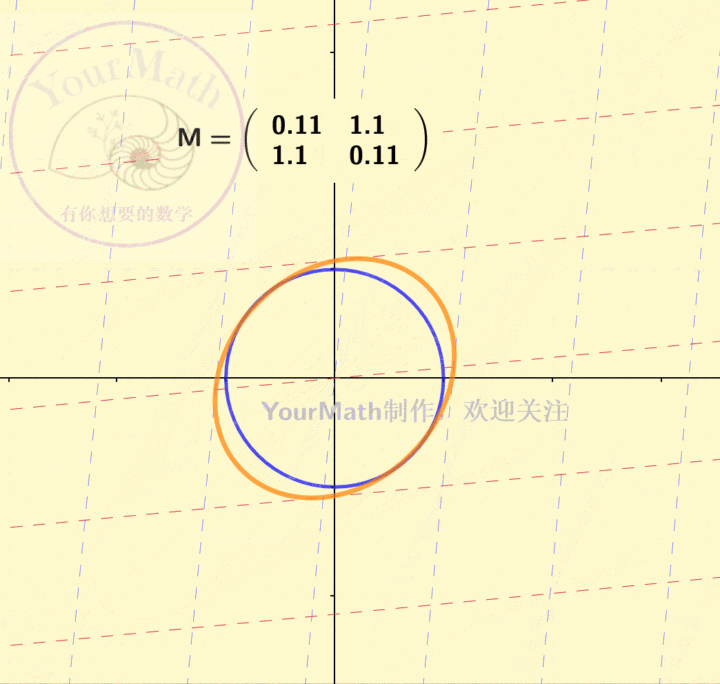
下图为一个双曲线经过不同的线性变换后的图像:
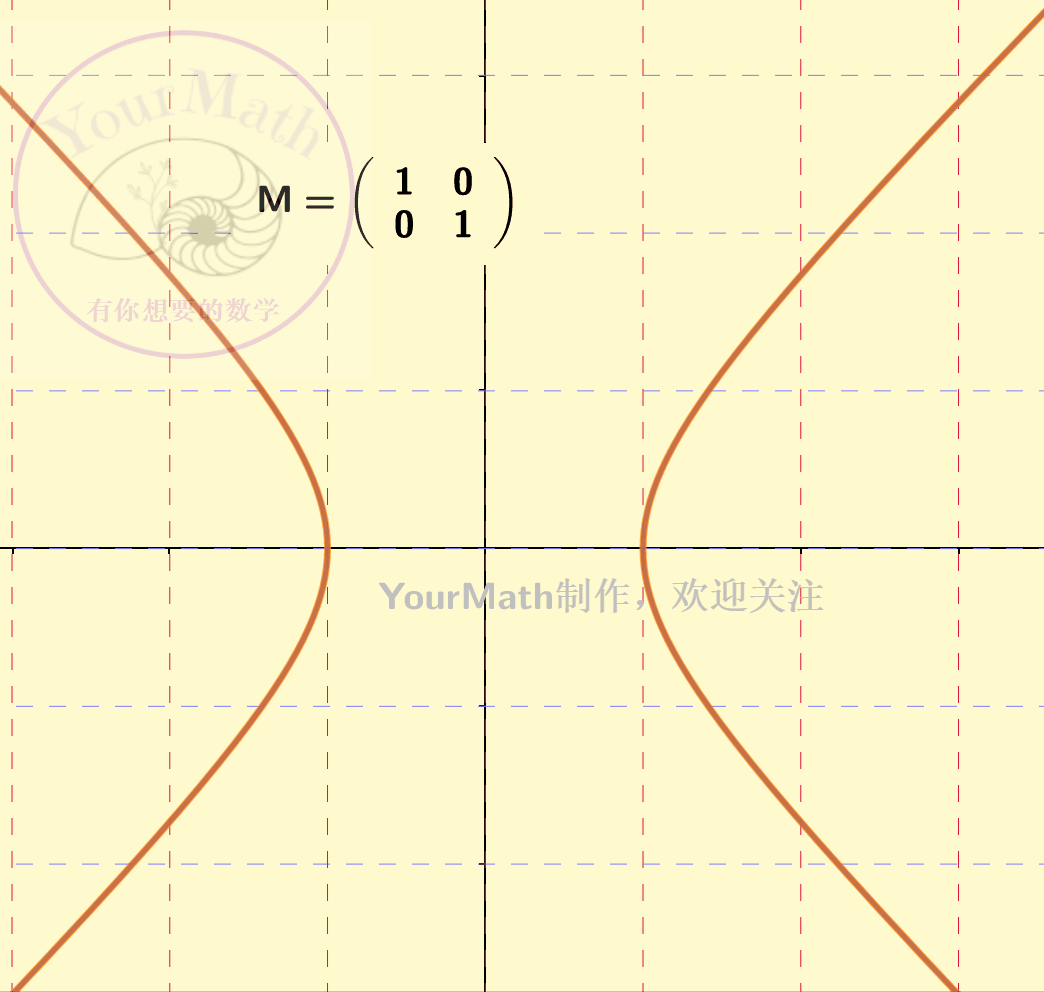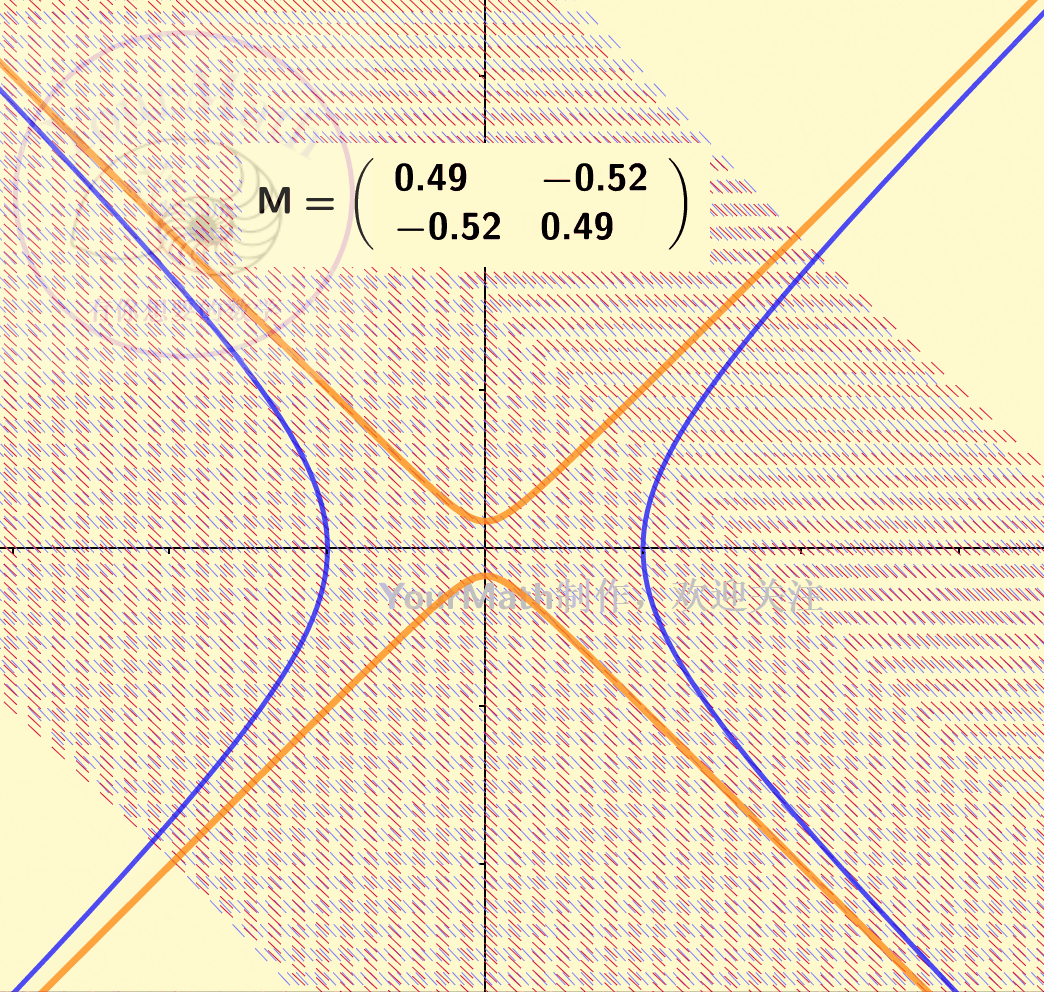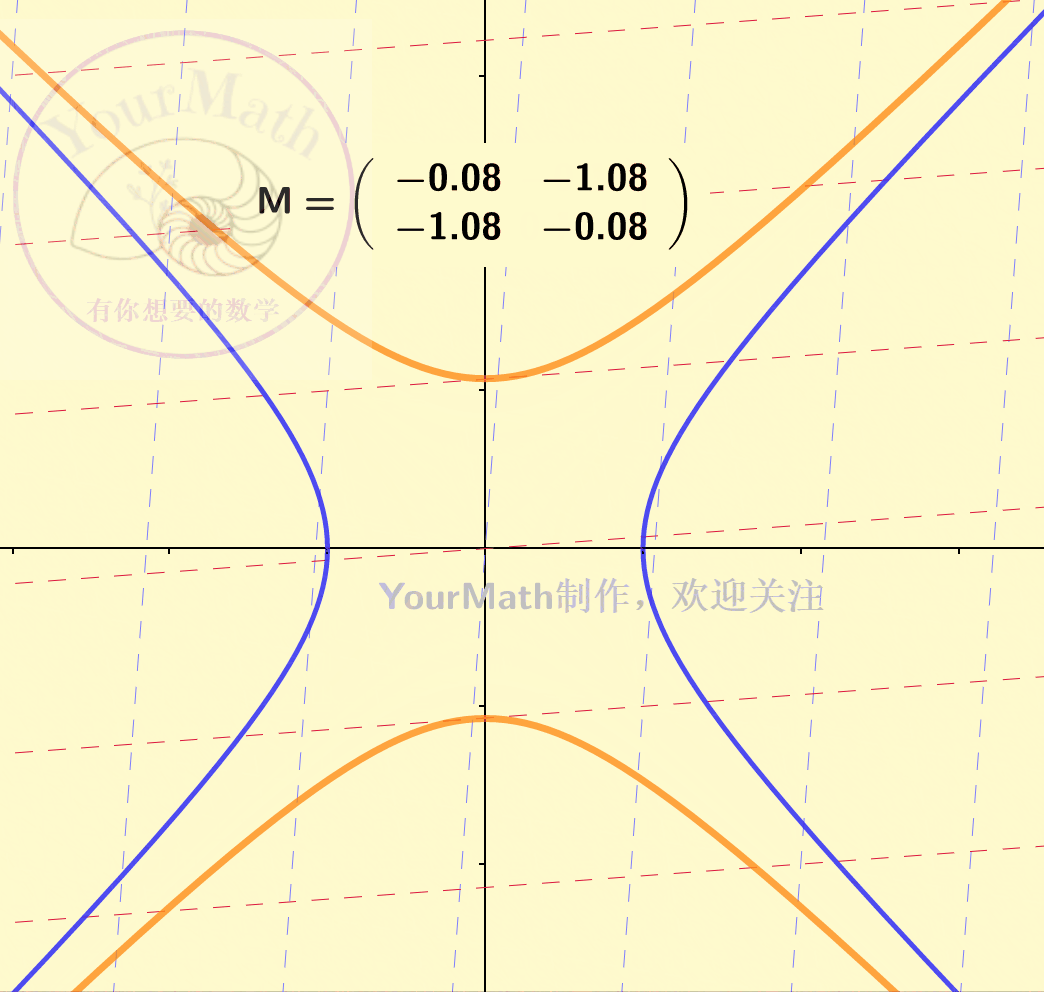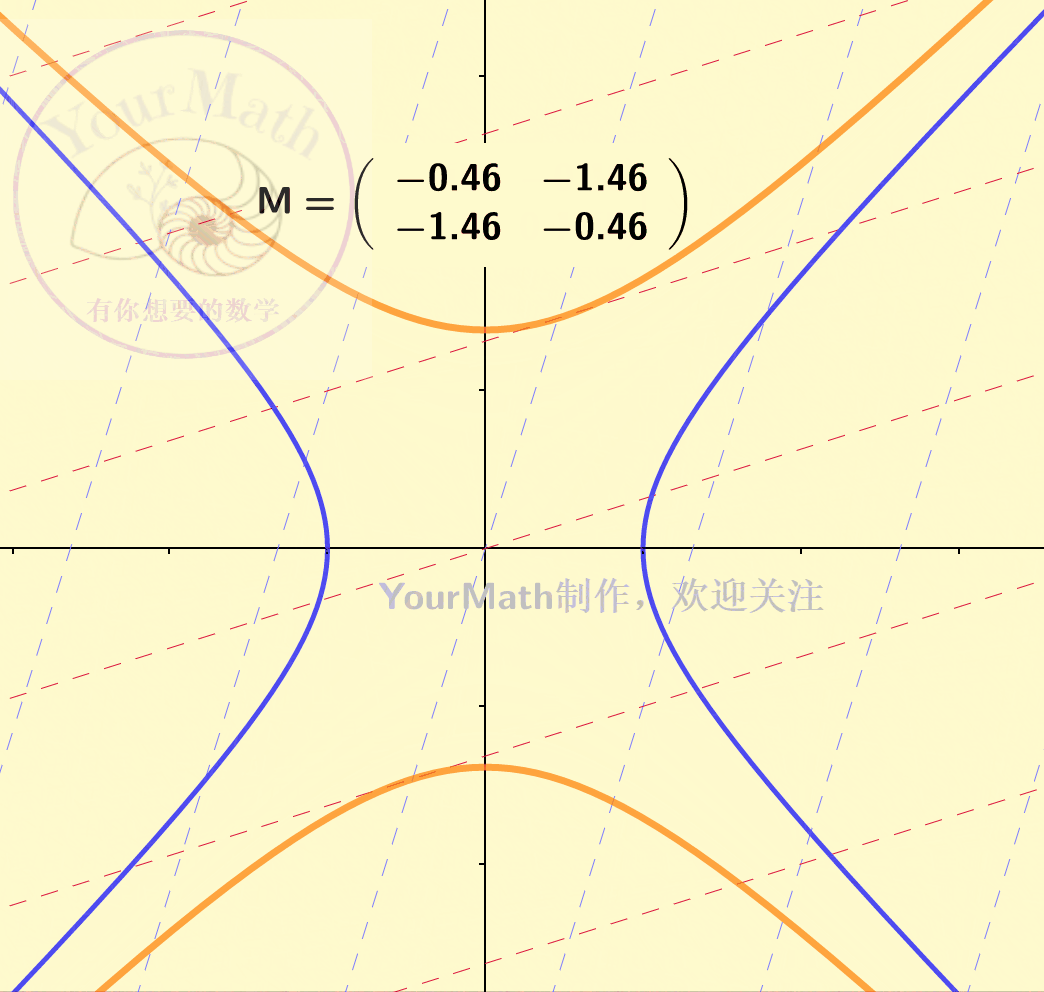
惯性定理,可以理解为任何一个椭圆/椭球/双曲线….在经过一个可逆的线性变换之后依然是一个椭圆/椭球/双曲线…。
