网页设计怎么做网站长沙公司网络营销推广

当需要百(千，万…)里挑一时，需要权衡最优解和效率，有一个37%原则比较有趣。

整个择优过程分为两个阶段：

• 观望：在前面$k$个候选者中冒泡记录最优者$p$，其分数为$V_p$，但并不选择。
• 选择：从第$k+1$个候选者开始，选择第一个满足$V_i>V_p$的候选者$i$，择优结束。

如果有10000个候选者，遍历10000次的过程中，越往后，找到比前面所有候选者都优秀的候选者的机会越渺茫，此时权衡一下概率和成本，就地抉择也不失为一种好策略，37%原则是这个问题的定量化表示。

总量$n$个候选人拍成一排，设停止观望的位置为$k$，从$k+1$到$n$的遍历比较，假设其中可以找到最有，设他的位置在$i$。

现在来看一下概率的计算：

• 总量$n$中选择一个$k$，有$\frac{1}{n}$种选择。
• $i$之前最优的人在前$k$个，有$\frac{k}{i-1}$种选择。
• 在$k$之后遍历所有的$i$，叠加所有可能性。
• 求出可能性最大的$k$值。

写成式子就是：

$P(k)=\sum _{i=k+1}^n\frac{1}{n}\frac{k}{i-1}=\frac{k}{n}\sum _{i=k+1}^n\frac{1}{i-1}$

为了求极值，用求导的方法，把离散求和式凑成连续的积分(这只是一种技巧，无必然)：

$P(k)=\frac{k}{n}{\int }_{k+1}^n\frac{1}{i-1}di=\frac{k}{n}(\ln (i-1){|}_{k+1}^n)$

进一步化简：

$P(k)=\frac{k}{n}(\ln (\frac{n-1}{k}))=-\frac{k}{n}\ln \frac{k}{n-1}\approx -\frac{k}{n}\ln \frac{k}{n}$

设$x=\frac{k}{n}$，则：

$P(nx)=-x\ln x$

设$f(x)=-x\ln x$，对$x$求导：

$f^{\prime }(x)=-\ln x-1$

得$x=\frac{1}{e}$时，$P$取最大值，此时：

$k=nx=0.37n$

$n$为总量，$k=0.37n$就是$n$的37%，这就是说，$k$达到总量的37%时，放弃观望后见优选择可以找到最优者的成功率最大，这个成功率是多少呢？

有趣的是，将$x=\frac{1}{e}$带入$f(x)$后：

$P(k)=f(x)=\frac{1}{e}\approx 0.37=37\%$

成功率最大的停止点在总量的37%处，成功率的值也是37%：

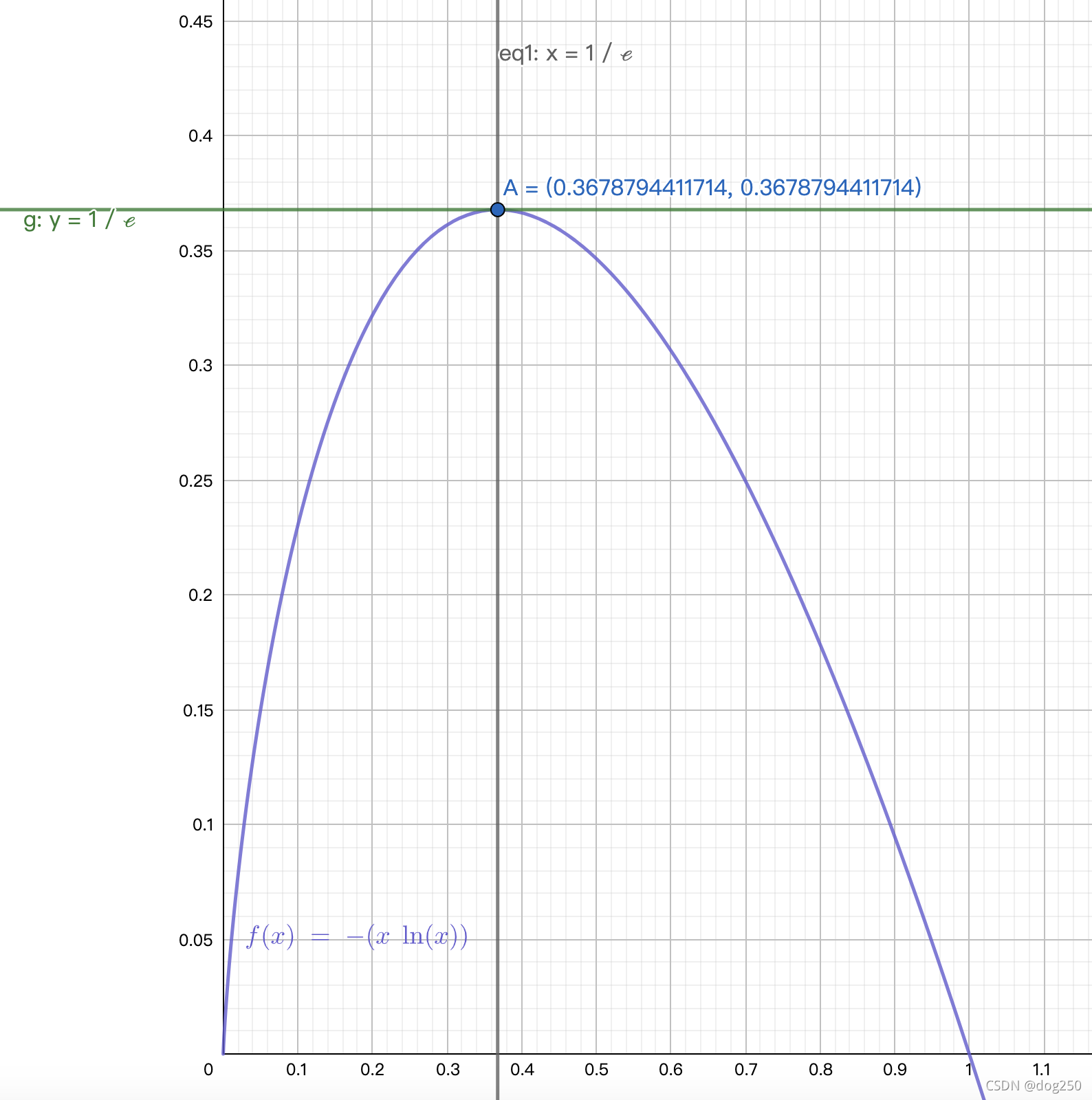
这也正是神奇的数学驻点$e$的又一个表现。

说回37%原则，事实上不光是百里挑一，发生在单向时间序列的人生亦如此，每一个决定都无法回头，同时亦无可能穷尽未来，选择最佳停止观望时机是一个普适问题，类似37%原则的最优停止原则还有很多，值得思考琢磨。

浙江温州皮鞋湿，下雨进水不会胖。