做网站的市场怎么样抖音seo关键词优化怎么做

解法一、dfs暴力法

/*题目描述
垒骰子
赌圣atm晚年迷恋上了垒骰子，就是把骰子一个垒在另一个上边，不能歪歪扭扭，
要垒成方柱体。经过长期观察，atm 发现了稳定骰子的奥秘；有些数字的面贴着
会互相排斥！
我们先来规范一下骰子：1 的对面是 4，2 的对面是 5，3 的对面是 6。
假设有 m 组互斥现象，每组中的那两个数字的面紧贴在一起，骰子就不能稳定的垒起来。 atm想计算一下有多少种不同的可能的垒骰子方式。
两种垒骰子方式相同，当且仅当这两种方式中对应高度的骰子的对应数字的朝向都相同。
由于方案数可能过多，请输出模 10^9 + 7 的结果。
不要小看了 atm 的骰子数量哦～「输入格式」
第一行两个整数 n m
n表示骰子数目
接下来 m 行，每行两个整数 a b ，表示 a 和 b 不能紧贴在一起。「输出格式」
一行一个数，表示答案模 10^9 + 7 的结果。「样例输入」
2 1
1 2
「样例输出」
544*/

这种暴力法只能提交到oj上只能通过30%的数据

package 第六届;import java.util.ArrayList;
import java.util.Scanner;public class 垒骰子 {static final long mod=1000000000+7;static int [][]a;static int atm[];//骰子对面 1-4  2-5 3-6static int duimian[]= {0,4,5,6,1,2,3};static int n;static long ans;static ArrayList []huchi;static long mypow(int x,int y) {long res=1;for(int i=1;i<=y;i++) {res*=x;}return res;}static void dfs(int r) {if(r==n) {ans++;return;}for(int i=1;i<=6;i++) {if(r>=1) {if(!huchi[ atm[r-1] ].contains(i)) {atm[r]=i;dfs(r+1);}}else {atm[r]=i;dfs(r+1);				}}}public static void main(String[] args) {Scanner reader=new Scanner(System.in);//n个骰子n=reader.nextInt();//m组互斥对int m=reader.nextInt();a=new int[m][2];atm=new int[n];huchi=new ArrayList[7];for(int i=1;i<=6;i++) {huchi[i]=new ArrayList();}//1 2 5//2 1 4//4*4  /*用链表记录互斥对数字* 1-4  2-5 3-6*/for(int i=0;i<m;i++) {int x=reader.nextInt();int y=reader.nextInt();			huchi[x].add(duimian[y]);huchi[y].add(duimian[x]);}dfs(0);//因为每个骰子四个面对应四种不同结果，所以还要乘上4^n//原题目：两种垒骰子方式相同，当且仅当这两种方式中对应高度的骰子的对应数字的朝向都相同。ans=( mypow(4,n)*ans)%mod;System.out.println(ans);}}

解法二、dp解法

提交到oj上也只能过70%的数据

package 第六届;import java.util.Scanner;public class 垒骰子_动态规划 {static final int mod=1000000000+7;static long mypow(int x,int y) {long res=1;for(int i=1;i<=y;i++) {res*=x;}return res;}public static void main(String[] args) {Scanner reader=new Scanner(System.in);//n个骰子int n=reader.nextInt();int m=reader.nextInt();//对立面int [] op=new int[] {0,4,5,6,1,2,3};//m组互斥对boolean [][] confilct=new boolean[7][7];for(int i=0;i<m;i++) {int x=reader.nextInt();int y=reader.nextInt();confilct[x][y]=true;confilct[y][x]=true;}//dp[i][j] 表示第i层 该层朝上数字为j时的可行方案数//由图中的递推式可知本层方案数目只与上一层有关 故可以用两行的动态数组保存方案数int [][] dp=new int[2][7];for(int i=1;i<=6;i++) {dp[0][i]=1;}//迭代的层数	for(int i=1;i<n;i++) {//面朝上的数字for(int j=1;j<=6;j++) {for(int x=1;x<=6;x++) {if(confilct[j][ op[x] ]) continue;dp[ i%2 ][j]=(dp[ i%2 ][j]+dp[(i-1)%2 ][x]);}}}long ans=0;for(int i=1;i<=6;i++) {ans+=dp[(n-1)%2][i];}ans=mypow(4,n)*ans%mod;System.out.println(ans);}}

解法三、矩阵快速幂

提交到oj上 终于可以全部通过了 关于矩阵的乘法运算和快速幂可以参考我的文章

package 第六届;
import java.util.Scanner;public class 垒骰子_矩阵乘法 {static int [] op=new int[7];static int n,m;private static final long mod=1000000000+7;static void init() {op[1]=4;op[2]=5;op[3]=6;op[4]=1;op[5]=2;op[6]=3;}public static void main(String[] args) {init();Scanner reader=new Scanner(System.in);n=reader.nextInt();m=reader.nextInt();long conflict[][]=new long[6][6];for(int i=0;i<6;i++) {for (int j = 0; j < 6; j++) {conflict[i][j]=1;}}//建立冲突矩阵for(int i=0;i<m;i++) {int x=reader.nextInt();int y=reader.nextInt();conflict[ op[x]-1 ][y-1]=0;conflict[ op[y]-1 ][x-1]=0;}//求冲突矩阵的n-1次方long [][] mPow_n_1=mPow(conflict,n-1);//累加mPow_n_1矩阵long ans=0;for(int i=0;i<6;i++) {for (int j = 0; j < 6; j++) {ans= ( ans+mPow_n_1[i][j] )%mod;}}System.out.println(ans*quick_Pow(4,n)%mod);
}//求i的n次方快速幂private static long quick_Pow(long i, int n) {long ret=1;while(n!=0) {if( (n&1)==1) {ret=(ret*i)%mod;}i=(i*i)%mod;n>>=1;}return ret;}/** 矩阵的快速幂*/private static long[][] mPow(long[][] conflict, int n) {long [][] ans=new long[6][6];//单位矩阵：对角线为1 其余皆为0for(int i=0;i<6;i++) {for(int j=0;j<6;j++) {if(i==j) {ans[i][j]=1;}else {ans[i][j]=0;}}}while(n!=0) {if((n&1)==1) {//该位上为1 ans矩阵与conflict矩阵相乘ans=mMul(ans,conflict);}conflict=mMul(conflict,conflict);//n右移一位 除以2n>>=1;}return ans;}//矩阵乘法private static long[][] mMul(long[][] a, long[][] b) {long [][] ans=new long[6][6];for(int i=0;i<6;i++) {for (int j = 0; j < 6; j++) {for (int k = 0; k < 6; k++) {ans[i][j]=( ans[i][j]+a[i][k]*b[k][j] )%mod;}}}return ans;}}

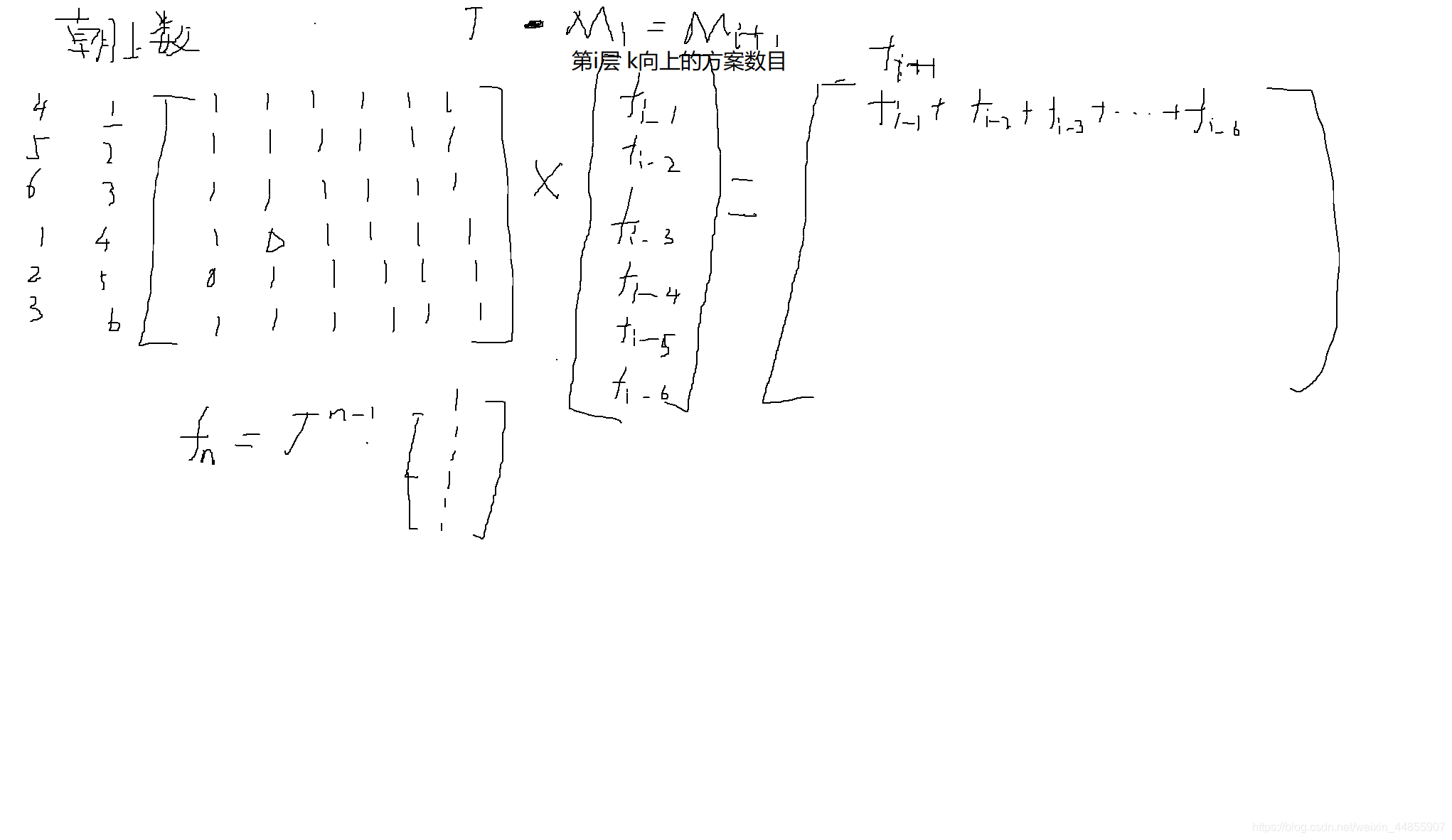
关于矩阵的幂运算和乘法，参见我博客快速幂和矩阵乘法