360网站排名怎么做搜索引擎网站优化推广
文章目录
- 如何分析一个“排序算法”?
- 排序算法的执行效率
- 排序算法的内存消耗
- 排序算法的稳定性
- 冒泡排序(Bubble Sort)
- 插入排序(Insertion Sort)
- 选择排序(Selection Sort)
- 解答开篇
- 课后思考
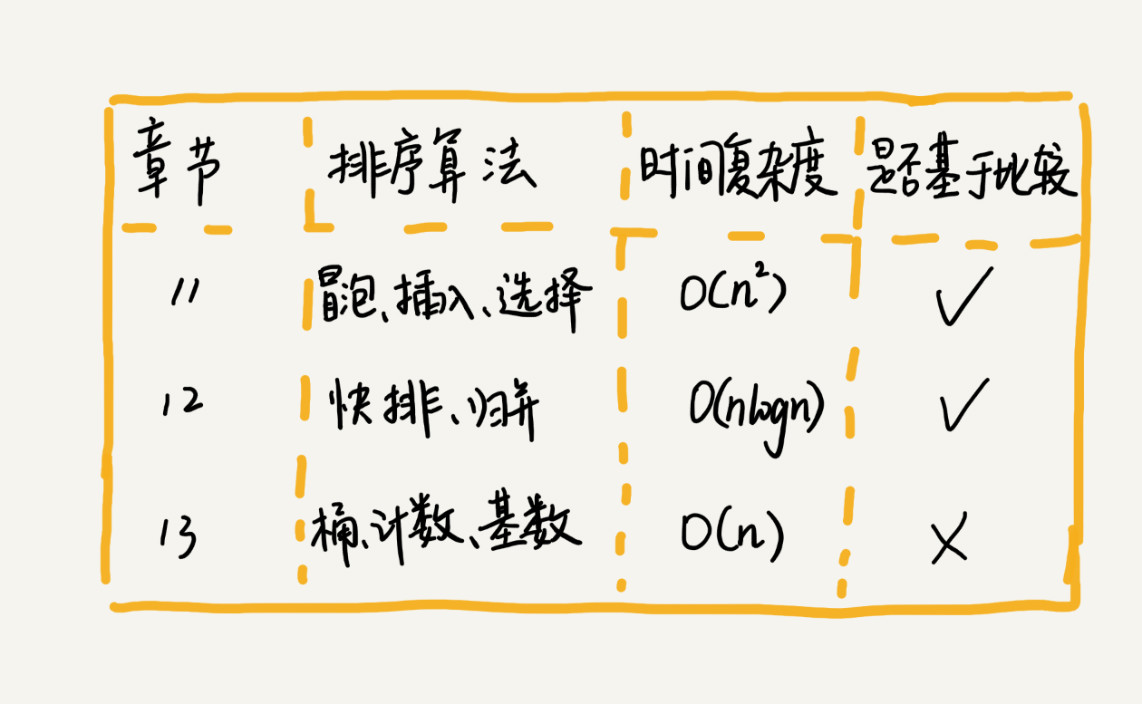
如何分析一个“排序算法”?
排序算法的执行效率
- 最好情况、最坏情况、平均情况时间复杂度
分别给出最好情况、最坏情况、平均情况下的时间复杂度以及最好、最坏时间复杂度对应的要排序的原始数据是什么样的。 - 时间复杂度的系数、常数 、低阶
- 比较次数和交换(或移动)次数
排序算法的内存消耗
原地排序算法,就是特指空间复杂度是 O(1) 的排序算法
排序算法的稳定性
如果待排序的序列中存在值相等的元素,经过排序之后,相等元素之间原有的先后顺序不变。
稳定排序算法可以保持金额相同的两个对象,在排序之后的前后顺序不变。
冒泡排序(Bubble Sort)
冒泡排序只会操作相邻的两个数据:
每次冒泡操作都会对相邻的两个元素进行比较,看是否满足大小关系要求。如果不满足就让它俩互换。一次冒泡会让至少一个元素移动到它应该在的位置,重复 n 次,就完成了 n 个数据的排序工作。


实际上,刚讲的冒泡过程还可以优化。当某次冒泡操作已经没有数据交换时,说明已经达到完全有序,不用再继续执行后续的冒泡操作。
实际上,刚讲的冒泡过程还可以优化。当某次冒泡操作已经没有数据交换时,说明已经达到完全有序,不用再继续执行后续的冒泡操作。

冒泡排序简单代码:
void bubbleSort(vector<int> &vec, int n){if(n < 2) return;for(int i = 0; i < n; ++i){bool tag = 0;for(int j = 0; j < n-i-1; ++j){if(a[j] > a[j+1]){ //交换int tmp = a[j];a[j] = a[j+1];a[j+1] = tmp;tag = 1; // 表示有数据交换}}if(!tag) break;}
}
-
第一,冒泡排序是原地排序算法吗?
冒泡的过程只涉及相邻数据的交换操作,只需要常量级的临时空间,所以它的空间复杂度为 O(1),是一个原地排序算法。 -
第二,冒泡排序是稳定的排序算法吗?
冒泡排序中,只有交换才可以改变两个元素的前后顺序。为了保证冒泡排序算法的稳定性,当有相邻的两个元素大小相等的时候,不做交换,相同大小的数据在排序前后不会改变顺序,所以冒泡排序是稳定的排序算法。 -
第三,冒泡排序的时间复杂度是多少?

那平均情况下的时间复杂是多少呢?
通过“有序度”和“逆序度”这两个概念来进行分析:
有序度是数组中具有有序关系的元素对的个数。有序元素对用数学表达式表示就是这样:
有序元素对:a[i] <= a[j], 如果i < j。

同理,对于一个倒序排列的数组,比如 6,5,4,3,2,1,有序度是 0;对于一个完全有序的数组,比如 1,2,3,4,5,6,有序度就是 n*(n-1)/2,也就是 15。我们把这种完全有序的数组的有序度叫作满有序度。
逆序度的定义正好跟有序度相反(默认从小到大为有序):
逆序元素对:a[i] > a[j], 如果i < j。
关于这三个概念,我们还可以得到一个公式:
逆序度=满有序度−有序度逆序度 = 满有序度 - 有序度逆序度=满有序度−有序度
排序的过程就是一种增加有序度,减少逆序度的过程,最后达到满有序度,就说明排序完成了。

冒泡排序包含两个操作原子,比较和交换:
每交换一次,有序度就加 1。不管算法怎么改进,交换次数总是确定的,即为逆序度(注意是交换次数),也就是n∗(n−1)/2n*(n-1)/2n∗(n−1)/2 – 初始有序度。此例中就是 15–3=12,要进行 12 次交换操作。
对于包含 n 个数据的数组进行冒泡排序,平均交换次数是多少呢?
- 最坏情况下,初始状态的有序度是 0,所以要进行 n∗(n−1)/2n*(n-1)/2n∗(n−1)/2次交换。
- 最好情况下,初始状态的有序度是 n∗(n−1)/2n*(n-1)/2n∗(n−1)/2,就不需要进行交换。
- 我们可以取个中间值 n∗(n−1)/4n*(n-1)/4n∗(n−1)/4,来表示初始有序度既不是很高也不是很低的平均情况。
换句话说,平均情况下,需要 n*(n-1)/4 次交换操作,比较操作肯定要比交换操作多,而复杂度的上限是 O(n^2),所以平均情况下的时间复杂度就是 O(n^2)。
插入排序(Insertion Sort)
一个有序的数组,往里面添加一个新的数据后,如何继续保持数据有序呢?很简单,只要遍历数组,找到数据应该插入的位置将其插入即可。

这是一个动态排序的过程,即动态地往有序集合中添加数据,我们可以通过这种方法保持集合中的数据一直有序。而对于一组静态数据,也可以借鉴上面讲的插入方法,来进行排序,于是就有了插入排序算法:
首先,将数组中的数据分为两个区间,已排序区间和未排序区间。初始已排序区间只有一个元素,就是数组的第一个元素。插入算法的核心思想是取未排序区间中的元素,在已排序区间中找到合适的插入位置将其插入,并保证已排序区间数据一直有序。重复这个过程,直到未排序区间中元素为空,算法结束:

插入排序也包含两种操作,一种是元素的比较,一种是元素的移动。当需要将一个数据 a 插入到已排序区间时,需要拿 a 与已排序区间的元素依次比较大小,找到合适的插入位置。找到插入点之后,还需要将插入点之后的元素顺序往后移动一位,这样才能腾出位置给元素 a 插入。
对于不同的查找插入点方法(从头到尾、从尾到头),元素的比较次数是有区别的。但对于一个给定的初始序列,移动操作的次数总是固定的,就等于逆序度。
为什么说移动次数就等于逆序度呢?拿刚才的例子画了一个图表,你一看就明白了。满有序度是 n*(n-1)/2=15,初始序列的有序度是 5,所以逆序度是 10。插入排序中,数据移动的个数总和也等于 10=3+3+4。

简单代码:
void insertionSort(vector<int> &vec, int n){if(n < 2) return;for(int i = 1; i < n; ++i){int value = a[i];int j = i-1;// 查找要插入的位置for(; j >= 0; --j){if(a[j] > value)a[j+1] = a[j]; //数据移动elsebreak;}a[j+1] = value; //插入数据}
}
-
第一,插入排序是原地排序算法吗?
从实现过程可以很明显地看出,插入排序算法的运行并不需要额外的存储空间,所以空间复杂度是 O(1),也就是说,这是一个原地排序算法。 -
第二,插入排序是稳定的排序算法吗?
对于值相同的元素,我们可以选择将后面出现的元素,插入到前面出现元素的后面,这样就可以保持原有的前后顺序不变,所以插入排序是稳定的排序算法。 -
插入排序的时间复杂度是多少?
如果要排序的数据已经是有序的,并不需要搬移任何数据。如果我们从尾到头在有序数据组里面查找插入位置,每次只需要比较一个数据就能确定插入的位置。所以这种情况下,最好是时间复杂度为 O(n)。
如果数组是倒序的,每次插入都相当于在数组的第一个位置插入新的数据,所以需要移动大量的数据,所以最坏情况时间复杂度为 O(n^2)。
还记得我们在数组中插入一个数据的平均时间复杂度是多少吗?没错,是 O(n)。所以,对于插入排序来说,每次插入操作都相当于在数组中插入一个数据,循环执行 n 次插入操作,所以平均时间复杂度为 O(n^2)。
选择排序(Selection Sort)
选择排序算法的实现思路有点类似插入排序,也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素,将其放到已排序区间的末尾。

-
第一,选择排序是原地排序算法吗?
选择排序空间复杂度为 O(1),是一种原地排序算法。选择排序的最好情况时间复杂度、最坏情况和平均情况时间复杂度都为 O(n^2)。 -
第二,选择排序是稳定的排序算法吗?
答案是否定的,选择排序是一种不稳定的排序算法。从前面的图中,可以看出,选择排序每次都要找剩余未排序元素中的最小值,并和前面的元素交换位置,这样破坏了稳定性。
比如 5,8,5,2,9 这样一组数据,使用选择排序算法来排序的话,第一次找到最小元素 2,与第一个 5 交换位置,那第一个 5 和中间的 5 顺序就变了,所以就不稳定了。正是因此,相对于冒泡排序和插入排序,选择排序就稍微逊色了。 -
插入排序的时间复杂度是多少?
选择排序的最好情况时间复杂度、最坏情况和平均情况时间复杂度都为 O(n^2)。
解答开篇
冒泡排序和插入排序的时间复杂度都是 O(n2),都是原地排序算法,为什么插入排序要比冒泡排序更受欢迎呢?
冒泡排序不管怎么优化,元素交换的次数是一个固定值,是原始数据的逆序度
插入排序是不管怎么优化,元素移动的次数也等于原始数据的逆序度
但是,从代码实现上来看,冒泡排序的数据交换要比插入排序的数据移动要复杂,冒泡排序需要 3 个赋值操作,而插入排序只需要 1 个。我们来看这段操作:
冒泡排序中数据的交换操作:
if (a[j] > a[j+1]) { // 交换int tmp = a[j];a[j] = a[j+1];a[j+1] = tmp;flag = true;
}插入排序中数据的移动操作:
if (a[j] > value) {a[j+1] = a[j]; // 数据移动
} else {break;
}
把执行一个赋值语句的时间粗略地计为单位时间(unit_time):
分别用冒泡排序和插入排序对同一个逆序度是 K 的数组进行排序。用冒泡排序,需要 K 次交换操作,每次需要 3 个赋值语句,所以交换操作总耗时就是 3*K 单位时间。而插入排序中数据移动操作只需要 K 个单位时间。
如果希望把性能优化做到极致,那肯定首选插入排序。

课后思考
特定算法是依赖特定的数据结构的。我们今天讲的几种排序算法,都是基于数组实现的。如果数据存储在链表中,这三种排序算法还能工作吗?如果能,那相应的时间、空间复杂度又是多少呢?
LeetCode第 147 题:对链表进行插入排序(C++)_qq_32523711的博客-CSDN博客
别人的答案:
对于老师所提课后题,觉得应该有个前提,是否允许修改链表的节点value值,还是只能改变节点的位置。
一般而言,考虑只能改变节点位置,冒泡排序相比于数组实现,比较次数一致,但交换时操作更复杂;插入排序,比较次数一致,不需要再有后移操作,找到位置后可以直接插入,但排序完毕后可能需要倒置链表;选择排序比较次数一致,交换操作同样比较麻烦。综上,时间复杂度和空间复杂度并无明显变化,若追求极致性能,冒泡排序的时间复杂度系数会变大,插入排序系数会减小,选择排序无明显变化。
