网络工程专业毕业论文宁波seo免费优化软件

在数学建模竞赛中，优化类题目是一个非常重要领域，占比一半以上。

优化类问题相对要难一些，主要就难在模型求解部分，本文来给大家介绍一些MATLAB求解数学规划模型的案例。

1、如何建立优化模型？

为了更直接地说明问题，我们先来看几个例子：

问题一：某工厂在计划期内要安排生产 I、II 两种产品，已知生产单位产品所需的设备台时及A、B两种原材料的消耗，如下表所示 

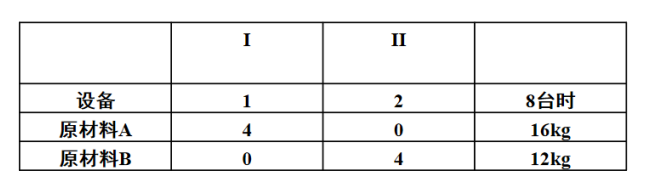
该工厂每生产一件产品I可获利2元，每生产一件产品II可获利3元。问应如何安排计划使该工厂获利最多？

所谓最优化问题是指使得问题中某一项指标“最优”的方案，”最优”包括：“最大”、“最小”、“最高”、“最低”、“最多”和“最少”等。解决优化问题第一步需要找到目标函数，也就是要找到“最优”；第二步需要寻找决策变量，也就是可以优化的变量，再通俗一点就是我们可以控制并使得目标函数更优的变量；第三步就是确定约束条件，在建模过程中比较难把握的就是约束条件，约束条件需要全面准确，否则会产生无穷多最优解或没有最优解，另外约束条件往往是对现实条件的数学刻画，对约束条件的合理简化也是比赛时候需要重点关注的地方。

在上面这个例子中，显然工厂利用就是目标函数，产品的生产计划就是决策变量，约束条件为原材料消耗和生产设备的使用时长，因此，其数学模型可表示为：

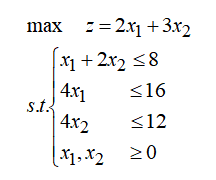
其中，x1,x2表示产品1和产品2的生产数量。

进一步，我们可以来总结一下优化问题的一般建模步骤：

Step1：确定决策变量；

Step2：用关于决策变量的函数表示目标，并确定是求极小还是极大；

Step3：明确约束条件，并用关于决策变量的数学语言表示；

Step4：根据变量的物理性质研究变量是否有非负性。

特别说明一下step4，这是建模过程中非常容易遗忘的一个点，像上文例子的第四条约束就反应了决策变量的非负性，因为我们知道根据物理性质，产品生产个数不能为负，其实这条约束仍然不是很严谨，产品个数不仅不能为负，同时还应该为整数，第四条约束应该为非负整数约束。

2、MATLAB求解线性规划模型

简单来说，约束条件和目标函数都是线性的，称之为线性规划，MATLAB求解线性规划的标准形式表示为：

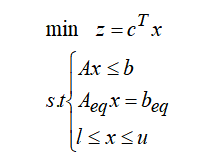
线性规划的求解可以通过MATLAB中的linprog函数来进行求解。其调用格式为:

[x,fval,exitflag] = linprog(fun,A,Aeq,beq,lb,ub,x0,options)

输入参数中，fun表示优化函数，x0表示优化的初始值，参数A、b为满足线性不等式约束的系数矩阵和结果向量，参数Aeq、beq为满足线性等式约束的系数矩阵和结果向量，lb、ub表示决策变量的取值范围，参数options为优化的各种属性，通过optimset函数进行设置。

输出参数中，x表示最优解，fval表示最优值，exitflag表示程序退出优化运算的类型，取值为-2,、-1、0、1、2、3、4、5，分别代表不同的异常类型，比如1表示程序运行成功。

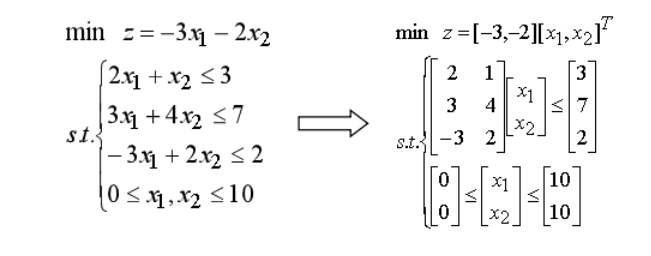
例程：

c=[-3,-2];A = [2,1;3,4;-3,2];b = [3;7;2];lb = [0;0];ub = [10;10];

[x,fval,exitflag] = linprog(c,A,b,[],[],lb,ub)

输出结果：

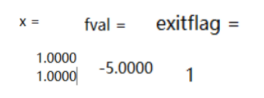
3、MATLAB求解非线性规划模型

对于非线性无约束优化，在MATLAB中可以采用fminsearch函数和fminunc函数进行求解，其调用格式为：

[x,fval,exitflag,output] = fminsearch(fun,x0,options)

输入参数：fun表示需要优化的目标函数，x0表示执行优化的初始数值，参数options为有优化的各种属性。

输出参数：x表示最优解，fval表示最优解队形的函数值，exitflag表示退出运算的原因，1表示收敛于最优解，0表示函数迭代次数超过设定阈值，output为结构体变量，显示优化的有关信息。

[x,fval,exitflag,output,grad,hessian] = fminunc(fun,x0,options)

输出参数中grad表示函数在返回的最优解处的梯度，hessian为最优解处的hessian矩阵。

例：求解函数f(x) = 100(x₂-x₁²)²+(1-x₁)²

function f = myfun(x)

    f = 100*(x(2) - x(1)^2)^2 + (1-x(1))^2;

end

x0 = [-0,0];[x,fval,exitflag,output] = fminsearch(@myfun,x0)

约束条件下的优化问题比无约束条件的优化问题要复杂的多，种类也比较多。对不同类型的优化问题，MATLAB提供了不同的优化方法。其中常用的是fmincon函数，调用格式为：

[x,fval,exitflag,output] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,options)

例：

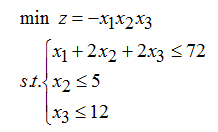
function f= optfun(x)

    f = -x(1)*x(2)*x(3);

End

x0 = [1,1,1];A = [1,2,2;0,1,0;0,0,1];b = [72;5;10];

[x,fval,exitflag,output] = fmincon(@optfun,x0,A,b)

4、总结

本文介绍了优化问题的一般建模方法及MATLAB中求解线性规划和非线性规划的常用命令，对于非线性规划还可以采用基于梯度的算法、基于概率搜索的算法、遗传算法等进行求解，在后续的文章中会陆续进行介绍。

~相关文章~

数学建模中的优化问题

经典优化算法大合集(比赛备用，值得收藏)

优化算法系列——模拟退火算法(1)

优化算法系列——模拟退火算法(2)——0-1背包问题

优化算法系列——遗传算法原理

优化算法系列——遗传算法MATLAB实例

优化算法系列——粒子群算法

优化算法系列——蚁群算法

优化算法系列——贪心算法

优化算法系列——最速下降法

优化算法系列——牛顿法

优化算法系列——共轭梯度法