廊坊做网站哪家好个人网站免费域名注册

对于一个给定的链表，返回环的入口节点，如果没有环，返回null 拓展： 你能给出不利用额外空间的解法么？

解题分两个步骤：

1. 首先，用快慢指针判断是否有环，有的话，返回相遇时节点
2. 两个指针分别从head和相遇的节点开始遍历，再次相遇时就是环的入口处节点

有一个证明过程：
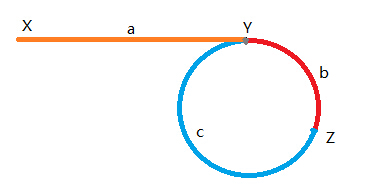
假设在Z处相遇，根据快指针是慢指针的速度两倍，可得出：
$$a+b+n(b+c)=2\ast (a+b)$$
即：
$$a=(n-1)\ast (b+c)+c$$
也就是说，若将两指针分别放在起始位置和相遇位置，并以相同速度前进，当一个指针走完距离a时，另一个指针恰好走出 绕环n-1圈加上c的距离。

/*** Definition for singly-linked list.* class ListNode {*     int val;*     ListNode next;*     ListNode(int x) {*         val = x;*         next = null;*     }* }*/
public class Solution {public ListNode detectCycle(ListNode head) {ListNode meetNode = checkCycle(head);if (meetNode == null) {return null;}ListNode slow = meetNode;ListNode fast = head;while (slow != fast) {slow = slow.next;fast = fast.next;}return slow;}public ListNode checkCycle(ListNode head) {ListNode slow = head;ListNode fast = head;while (fast != null && fast.next != null) {fast = fast.next.next;slow = slow.next;if (fast == slow) {return fast;}}return null;}
}