政府网站建设公司西安关键词快速排名
1、k-armed bandit problem
首先符号定义:
AtA_tAt:在时间 t 时选择的动作
RtR_tRt:在时间 t 时获得的相应的reward
q∗(a)q_*(a)q∗(a):随机动作 a 的值(期望奖励),公式如下:
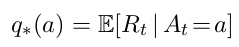
如果q∗(a)q_*(a)q∗(a)已知,k-armed bandit problem就变的很简单了,只需要选择值最高的动作就行。
如果q∗(a)q_*(a)q∗(a)不确定,可用估计值来表示。将动作 a 在 t 时刻的估计表示为:
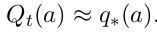
2、action-value methods
一种简单的估计值的方法:平均实际获得的奖励(估计动作值的平均样本法)。该方法适用于稳定的环境。

其中:
1Ai=a1_{A_i=a}1Ai=a 表示 Ai=a{A_i=a}Ai=a 时为 1 ,否则为 0 ;
如果分母为 0 ,则将 Qt(a)Q_t(a)Qt(a) 定义为某个默认值,比如 Q1(a)=0Q_1(a)=0Q1(a)=0 ;
如果分母趋于无穷时,根据大数定律, Qt(a)Q_t(a)Qt(a) 收敛到 q∗(a)q_*(a)q∗(a) 。
1) 最简单的动作选择方法:
选择具有最高估计动作值的动作(At∗A_t^*At∗)—— greedy action
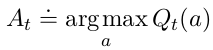
2) ϵ\epsilonϵ -greedy 方法:
每隔一段时间,有 ϵ\epsilonϵ 的概率随机选择动作。
优点:在极限状态下,随着步数的增加,每个动作将被采样无数次,从而保证 Qt(a)Q_t(a)Qt(a) 收敛到 q∗(a)q_*(a)q∗(a) 。这意味着选择最优动作的概率收敛到大于 1 - ϵ\epsilonϵ 。
3、Incremental Implementation
以一种计算概率的方式来计算期望。
RiR_iRi:第 i 次选择某一动作后得到的奖励;
QnQ_nQn:n-1 次后的动作值的估计:
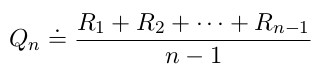
代码实现该函数时需要考虑存储奖励所需的内存大小和计算量。
将上面的公式进行推导,变成增量形式的公式,用于更新平均值。这样使得每个新奖励所需的计算量很小且恒定。

下面给出一个简单的 bandit 算法:
 注:一般可用 α=1/n\alpha=1/nα=1/n 或者 αt(A)\alpha_t(A)αt(A) 来表示。
注:一般可用 α=1/n\alpha=1/nα=1/n 或者 αt(A)\alpha_t(A)αt(A) 来表示。
4、Tracking a Nonstationary Problem
在不稳定环境中,将最近获得的奖励看得比过去的更加重要。最常用的方法之一是使用常数步长参数。
Qn+1Q_{n+1}Qn+1 是 Q1Q_1Q1 和 RiR_iRi 的加权平均:

5、Optimistic Initial Values
前面的方法均在一定程度上依赖于最初的动作值估计:Q1(a)Q_1(a)Q1(a) 。可以选择较好的值来初始化也是一种不错的方法,但是不适用在不稳定的环境中。
6、Upper-Confidence-Bound Action Selection(UCB)
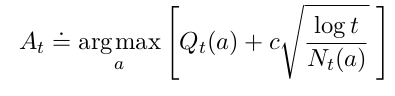
缺点:1)在不稳定的环境中可能会很复杂;2)状态空间很大时也可能不适用。
7、Gradient Bandit Algorithms
考虑学习每个动作 aaa 的数值偏好 Ht(a)H_t(a)Ht(a) , Ht(a)H_t(a)Ht(a)越大,采取动作的频率越高,但偏好并不能解释奖励。
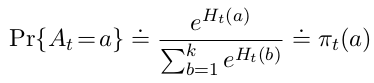
Ht(a)H_t(a)Ht(a) 使用梯度上升算法:
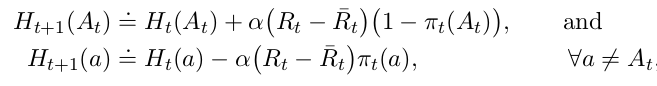
其中,α\alphaα 为步长参数,R‾t∈R{\overline{R}_t}\in\RRt∈R 为时间 t 内所有奖励的平均。
10-armed bandit problem的python实现
import numpy as np
import matplotlib.pyplot as plt
import randomsteps = 10000
armNum = 10
e_greedy = 0.01
totalReward = np.zeros(steps)# 每个动作的奖励的均值
mean_qa = np.array([0.2, -0.3, 1.5, 0.5, 1.2, -1.6, -0.2, -1, 1.1, -0.6])
# 每个动作的奖励的方差
var_qa = np.array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1])def get_reward(a):r = np.random.normal(mean_qa[a], var_qa[a], 1)return r[0]def main():# 初始化Q(a)和N(a)Qa = np.zeros(armNum)actionN = np.zeros(armNum)# repeatfor t in range(1, steps):# choose an actionif np.random.uniform() < 1-e_greedy:index = np.where(Qa == np.max(Qa))action = random.sample(index, 1)else:# choose random actionaction = random.randrange(9)# get a rewardr = get_reward(action)# updateactionN[action] += 1Qa[action] = Qa[action] + 1/actionN[action]*(r - Qa[action])# record the average of rewardstotalReward[t] = ((t-1)*totalReward[t-1] + r) / tx = np.linspace(1, steps, steps)plt.plot(x, totalReward)plt.legend()print(Qa)plt.show()if __name__ == '__main__':main()
