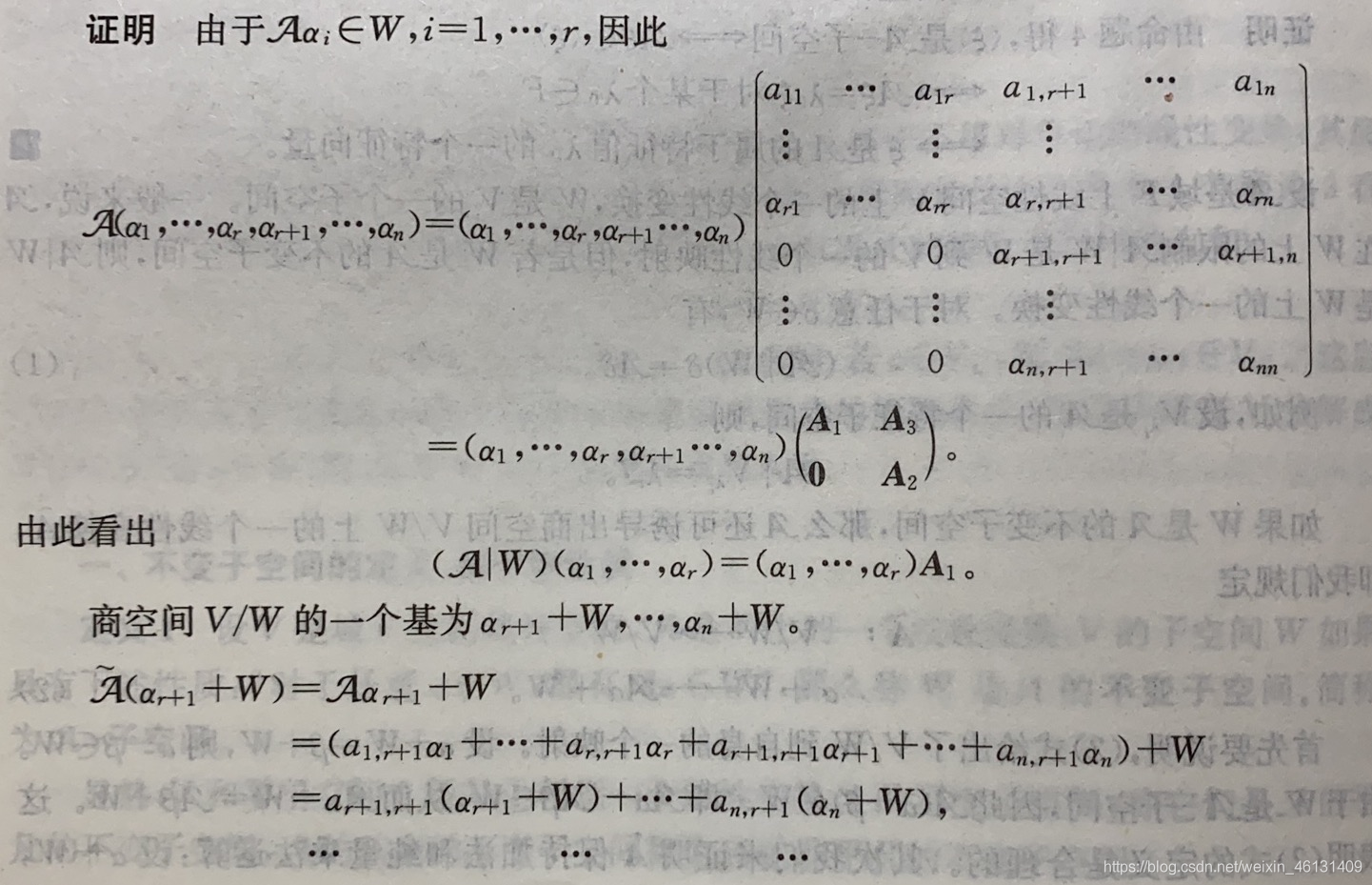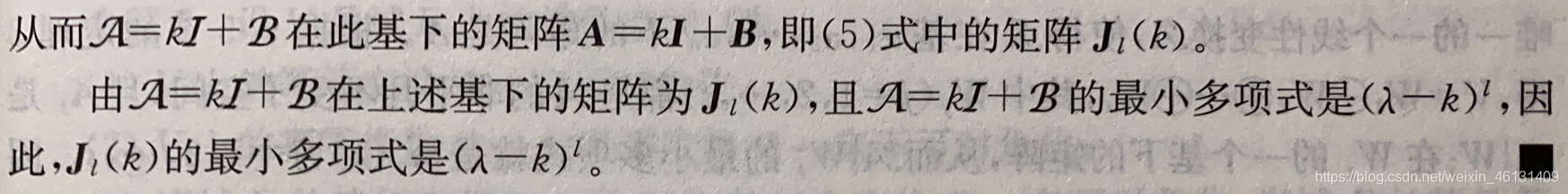武汉平台网站建设 APP贴吧推广
一.不变子空间与Hamilton−CayleyHamilton-CayleyHamilton−Cayley定理(9.5)

1.不变子空间
(1)概念:

(2)性质与判定:
命题1:VVV上线性变换ᎯᎯᎯ的核与象,ᎯᎯᎯ的特征子空间都是Ꭿ−Ꭿ-Ꭿ−子空间
命题2:设Ꭿ,BᎯ,ℬᎯ,B都是VVV上的线性变换,如果Ꭿ,BᎯ,ℬᎯ,B可交换,那么KerB,ImB,BKer\,ℬ,Im\,ℬ,ℬKerB,ImB,B的特征子空间都是Ꭿ−Ꭿ-Ꭿ−子空间
推论1:设ᎯᎯᎯ是域FFF上线性空间VVV上的线性变换,f(x)∈F[x]f(x)∈F[x]f(x)∈F[x],则Kerf(Ꭿ),Imf(Ꭿ),f(Ꭿ)Ker\,f(Ꭿ),Im\,f(Ꭿ),f(Ꭿ)Kerf(Ꭿ),Imf(Ꭿ),f(Ꭿ)的特征子空间都是Ꭿ−Ꭿ-Ꭿ−子空间
命题3:VVV上线性变换ᎯᎯᎯ的不变子空间的和与交仍是ᎯᎯᎯ的不变子空间
命题4:设ᎯᎯᎯ是域FFF上线性空间VVV上的1个线性变换,W=<α1,α2...αs>W=<α_1,α_2...α_s>W=<α1,α2...αs>是VVV的1个子空间,则WWW是Ꭿ−Ꭿ-Ꭿ−子空间当且仅当Ꭿαi∈W(i=1,2...s)Ꭿα_i∈W\,(i=1,2...s)Ꭿαi∈W(i=1,2...s)
命题5:设ᎯᎯᎯ是域FFF上线性空间VVV上的1个线性变换,ξ∈V\xi∈Vξ∈V且ξ≠0\xi≠0ξ=0,则<ξ><\xi><ξ>是Ꭿ−Ꭿ-Ꭿ−子空间当且仅当ξ\xiξ是ᎯᎯᎯ的1个特征向量
(3)将线性变换限制到不变子空间或其商空间上:


2.用不变子空间研究线性变换的矩阵表示
(1)将线性变换表示成分块上三角矩阵:
定理1:设A\mathcal{A}A是域FFF上nnn维线性空间VVV上的1个线性变换,WWW是A\mathcal{A}A的1个非平凡的不变子空间WWW中取1个基α1...αrα_1...α_rα1...αr,把它扩充成VVV的1个基α1...αr,αr+1...αnα_1...α_r,α_{r+1}...α_nα1...αr,αr+1...αn,则A\mathcal{A}A在此基下的矩阵AAA为1个分块上三角矩阵A=[A1A30A2]A=\left[\begin{matrix}A_1&A_3\\0&A_2\end{matrix}\right]A=[A10A3A2]其中A1A_1A1是A∣W\mathcal{A}\,|\,WA∣W在WWW的1个基α1...αrα_1...α_rα1...αr下的矩阵,A2A_2A2是A\mathcal{A}A诱导的商空间V/WV/WV/W上的线性变换A~\tilde{\mathcal{A}}A~在V/WV/WV/W的1个基αr+1+W...αn+Wα_{r+1}+W...α_n+Wαr+1+W...αn+W下的矩阵;设A,A∣W,A~\mathcal{A},\mathcal{A}\,|\,W,\tilde{\mathcal{A}}A,A∣W,A~的特征多项式分别为f(λ),f1(λ),f2(λ)f(λ),f_1(λ),f_2(λ)f(λ),f1(λ),f2(λ),则f(λ)=f1(λ)f2(λ)f(λ)=f_1(λ)f_2(λ)f(λ)=f1(λ)f2(λ)
定理2:设A\mathcal{A}A是域FFF上nnn维线性空间VVV上的1个线性变换,如果A\mathcal{A}A在VVV的1个基α1...αr,αr+1...αnα_1...α_r,α_{r+1}...α_nα1...αr,αr+1...αn下的矩阵AAA为分块上三角矩阵A=[A1A30A2]A=\left[\begin{matrix}A_1&A_3\\0&A_2\end{matrix}\right]A=[A10A3A2]令W=<α1...αr>W=<α_1...α_r>W=<α1...αr>,那么WWW是A\mathcal{A}A的1个非平凡不变子空间,且A∣W\mathcal{A}\,|\,WA∣W在WWW的1个基α1...αrα_1...α_rα1...αr下的矩阵是A1A_1A1
(2)将线性变换表示成分块对角矩阵:
定理3:设A\mathcal{A}A是域FFF上nnn维线性空间VVV上的1个线性变换,则A\mathcal{A}A在VVV的1个基下的矩阵为分块对角矩阵(3)当且仅当VVV能分解成A\mathcal{A}A的非平凡不变子空间的直和:V=W1⊕W2⊕...⊕WsV=W_1\oplus W_2\oplus...\oplus W_sV=W1⊕W2⊕...⊕Ws,并且AiA_iAi是A∣Wi\mathcal{A}\,|\,W_iA∣Wi在WiW_iWi的1个基下的矩阵
(3)寻找线性变换的非平凡不变子空间:

引理:设VVV是域FFF上的线性空间(可以是有限维的,也可以是无限维的),A\mathcal{A}A是VVV上的1个线性变换,在F[x]F[x]F[x]中,f(x)=f1(x)f2(x)f(x)=f_1(x)f_2(x)f(x)=f1(x)f2(x),且(f1(x),f2(x))=1(f_1(x),f_2(x))=1(f1(x),f2(x))=1,则Kerf(A)=Kerf1(A)⊕Kerf2(A)(5)Ker\,f(\mathcal{A})=Ker\,f_1(\mathcal{A})\oplus Ker\,f_2(\mathcal{A})\qquad(5)Kerf(A)=Kerf1(A)⊕Kerf2(A)(5)
定理4:设VVV是域FFF上的线性空间(可以是有限维的,也可以是无限维的),A\mathcal{A}A是VVV上的1个线性变换,在F[x]F[x]F[x]中:f(x)=f1(x)f2(x)...fs(x)(9)f(x)=f_1(x)f_2(x)...f_s(x)\qquad(9)f(x)=f1(x)f2(x)...fs(x)(9)其中f1(x),f2(x)...fs(x)f_1(x),f_2(x)...f_s(x)f1(x),f2(x)...fs(x)两两互素,则Kerf(A)=Kerf1(A)⊕Kerf2(A)⊕...⊕Kerfs(A)(10)Ker\,f(\mathcal{A})=Ker\,f_1(\mathcal{A})\oplus Ker\,f_2(\mathcal{A})\oplus...\oplus Ker\,f_s(\mathcal{A})\qquad(10)Kerf(A)=Kerf1(A)⊕Kerf2(A)⊕...⊕Kerfs(A)(10)
3.零化多项式:

4.哈密顿-凯莱定理(Hamilton-Cayley Theorem)

(1)整环上的矩阵:

(2)Hamilton−CayleyHamilton-CayleyHamilton−Cayley定理:
定理5:设AAA是域FFF上的nnn级矩阵,则AAA的特征多项式f(λ)f(λ)f(λ)是AAA的1个零化多项式,从而域FFF上nnn维线性空间VVV上的线性变换A\mathcal{A}A的特征多项式f(λ)f(λ)f(λ)是A\mathcal{A}A的1个零化多项式
(3)利用Hamilton−CayleyHamilton-CayleyHamilton−Cayley定理分解线性变换:

二.最小多项式(9.6)

1.定义与性质
(1)线性变换的最小多项式:

域FFF上线性空间VVV上的线性变换A\mathcal{A}A的最小多项式通常记为m(λ)m(λ)m(λ)
(2)线性变换的最小多项式的性质:
命题6:线性空间VVV上的线性变换A\mathcal{A}A的最小多项式是唯一的
命题7:设A\mathcal{A}A是域FFF上线性空间VVV上的线性变换,F[λ]F[λ]F[λ]中的多项式g(λ)g(λ)g(λ)是A\mathcal{A}A的零化多项式当且仅当g(λ)g(λ)g(λ)是A\mathcal{A}A的最小多项式m(λ)m(λ)m(λ)的倍式
命题8:设A\mathcal{A}A是域FFF上线性空间VVV上的线性变换,则A\mathcal{A}A的最小多项式m(λ)m(λ)m(λ)与A\mathcal{A}A的特征多项式f(λ)f(λ)f(λ)在FFF中有相同的根(但重数可以不同)
推论1:设A\mathcal{A}A是域FFF上nnn维线性空间VVV上的线性变换,域E⊇FE\supe FE⊇F,则A\mathcal{A}A的最小多项式m(λ)m(λ)m(λ)与A\mathcal{A}A的特征多项式f(λ)f(λ)f(λ)在EEE中有相同的根(但重数可以不同)
(3)矩阵的最小多项式:

命题8’:域FFF上nnn级矩阵AAA的最小多项式m(λ)m(λ)m(λ)与AAA的特征多项式f(λ)f(λ)f(λ)在FFF中有相同的根(但重数可以不同)
推论1:相似的矩阵有相同的最小多项式
推论2:设AAA是域FFF上的nnn级矩阵,域E⊇FE\supe FE⊇F,则AAA的最小多项式m(λ)m(λ)m(λ)与AAA的特征多项式f(λ)f(λ)f(λ)在EEE中有相同的根(但重数可以不同)
(4)矩阵的最小多项式不随域的扩大而改变:

命题9:设AAA是域FFF上的矩阵,域E⊇FE\supe FE⊇F,则如果m(λ)m(λ)m(λ)是AAA的最小多项式,那么把AAA看成域EEE上的矩阵,其最小多项式仍是m(λ)m(λ)m(λ)
2.几类特殊线性变换或矩阵的最小多项式
(1)几类特殊的最小多项式:


(2)约当块(Jordan Block):
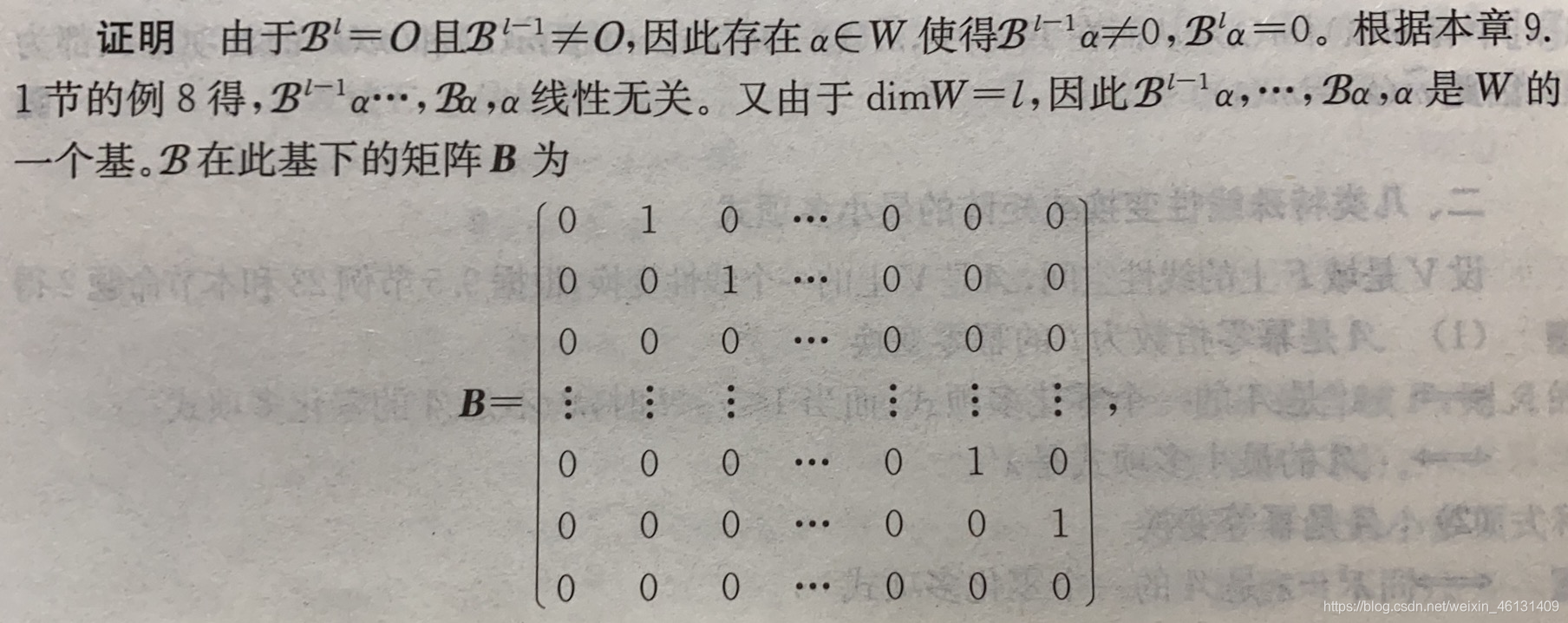
命题10:设A\mathcal{A}A是域FFF上lll维线性空间WWW上的线性变换,如果A=kI+B\mathcal{A}=k\mathcal{I}+\mathcal{B}A=kI+B,其中B\mathcal{B}B是幂零指数为lll的幂零变换,那么WWW中存在1个基使得A\mathcal{A}A在此基下的矩阵AAA为A=[k10...0000k1...00000k...000.....................000...k10000...0k1000...00k](5)A=\left[\begin{matrix}k&1&0&...&0&0&0\\0&k&1&...&0&0&0\\0&0&k&...&0&0&0\\...&...&...&...&...&...&...\\0&0&0&...&k&1&0\\0&0&0&...&0&k&1\\0&0&0&...&0&0&k\end{matrix}\right]\qquad(5)A=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡k00...0001k0...00001k...000.....................000...k00000...1k0000...01k⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤(5)把(5)式中的矩阵称为1个lll级约当块,记作Jl(k)J_l(k)Jl(k),其中kkk是主对角线上的元素;于是Jl(k)J_l(k)Jl(k)的最小多项式是(λ−k)l(λ-k)^l(λ−k)l
推论1:域FFF上的lll级矩阵AAA相似于Jl(k)J_l(k)Jl(k)当且仅当AAA的最小多项式为(λ−k)l(λ-k)^l(λ−k)l
(3)线性变换在线性空间与不变子空间上的最小多项式间的关系:
定理6:设A\mathcal{A}A是域FFF上线性空间VVV上的线性变换,如果VVV能分解成A\mathcal{A}A的一些非平凡不变子空间的直和:V=W1⊕W2⊕...⊕Ws(6)V=W_1\oplus W_2\oplus...\oplus W_s\qquad(6)V=W1⊕W2⊕...⊕Ws(6)那么A\mathcal{A}A的最小多项式m(λ)m(λ)m(λ)为m(λ)=[m1(λ),m2(λ)...ms(λ)](7)m(λ)=[m_1(λ),m_2(λ)...m_s(λ)]\qquad(7)m(λ)=[m1(λ),m2(λ)...ms(λ)](7)其中mi(λ)(i=1,2...s)m_i(λ)\,(i=1,2...s)mi(λ)(i=1,2...s)是Wj(j=1,2...s)W_j\,(j=1,2...s)Wj(j=1,2...s)上的线性变换A∣Wj\mathcal{A}\,|\,W_jA∣Wj的最小多项式;[m1(λ),m2(λ)...ms(λ)][m_1(λ),m_2(λ)...m_s(λ)][m1(λ),m2(λ)...ms(λ)]是m1(λ),m2(λ)...ms(λ)m_1(λ),m_2(λ)...m_s(λ)m1(λ),m2(λ)...ms(λ)的最小公倍式
推论1:设AAA是域FFF上的1个nnn级分块对角矩阵,即A=diag{A1,A2...As}A=diag\{A_1,A_2...A_s\}A=diag{A1,A2...As},设AjA_jAj的最小多项式是mj(λ)(j=1,2...s)m_j(λ)\,(j=1,2...s)mj(λ)(j=1,2...s),则AAA的最小多项式m(λ)m(λ)m(λ)为m(λ)=[m1(λ),m2(λ)...ms(λ)]m(λ)=[m_1(λ),m_2(λ)...m_s(λ)]m(λ)=[m1(λ),m2(λ)...ms(λ)]
(4)约当形矩阵(Jordan Matrix):

3.用最小多项式研究线性变换的矩阵表示
(1)线性变换可对角化的条件:
定理7:设A\mathcal{A}A是域FFF上nnn维线性空间VVV上的线性变换,则A\mathcal{A}A可对角化当且仅当A\mathcal{A}A的最小多项式m(λ)m(λ)m(λ)在F[λ]F[λ]F[λ]中能分解成不同的1次因式的乘积
推论1:域FFF上的nnn级矩阵AAA可对角化当且仅当AAA的最小多项式m(λ)m(λ)m(λ)在F[λ]F[λ]F[λ]中能分解成不同的1次因式的乘积
定理7及其推论使许多特殊类型的线性变换和矩阵是否可对角化的判定变得非常简洁
(2)最小多项式与可对角化的线性变换:
命题11:设VVV是域FFF上的线性空间,则
①VVV上的幂等变换A\mathcal{A}A一定可对角化
②VVV上的幂零指数l>1l>1l>1的幂零变换A\mathcal{A}A一定不可对角化
③当域FFF的特征不等于2时,VVV上的对合变换A\mathcal{A}A一定可对角化;当域FFF的特征等于2时,不等于I\mathcal{I}I的对合变换A\mathcal{A}A一定不可对角化
④当FFF是复数域时,VVV上的周期变换一定可对角化
命题12:域FFF是级数r>1r>1r>1的约当块Jr(a)J_r(a)Jr(a)一定不可对角化;包含级数大于1的约当块的约当形矩阵一定不可对角化
推论1:设A\mathcal{A}A是域FFF上nnn维线性空间VVV上的线性变换,如果A\mathcal{A}A可对角化,那么对于A\mathcal{A}A的任意1个非平凡不变子空间WWW都有A∣W\mathcal{A}\,|\,WA∣W可对角化
(3)最小多项式与不可对角化的线性变换:



\quad\\\quad
附录.利用命题12的推论1确定可对角化的线性变换的不变子空间的结构
命题13:设A\mathcal{A}A是域FFF上nnn维线性空间VVV上的线性变换,如果A\mathcal{A}A可对角化,且λ1,λ2...λsλ_1,λ_2...λ_sλ1,λ2...λs是A\mathcal{A}A的所有不同的特征值,那么A\mathcal{A}A的任一非平凡不变子空间WWW为W=(Vλj1∩W)⊕(Vλj2∩W)⊕...⊕(Vλjr∩W)W=(V_{λ_{j_1}}∩W)\oplus(V_{λ_{j_2}}∩W)\oplus...\oplus(V_{λ_{j_r}}∩W)W=(Vλj1∩W)⊕(Vλj2∩W)⊕...⊕(Vλjr∩W)其中λj1,λj2...λjrλ_{j_1},λ_{j_2}...λ_{j_r}λj1,λj2...λjr是A\mathcal{A}A的rrr个不同的特征值,并且对于Vλji(i=1,2...s)V_{λ_{j_i}}\,(i=1,2...s)Vλji(i=1,2...s),存在A\mathcal{A}A的不变子空间UjrU_{j_r}Ujr,使得Vλji=(Vλji∩W)⊕UλjiV_{λ_{j_i}}=(V_{λ_{j_i}}∩W)\oplus U_{λ_{j_i}}Vλji=(Vλji∩W)⊕Uλji
命题14:设A\mathcal{A}A是域FFF上nnn维线性空间VVV上的线性变换,则A\mathcal{A}A可对角化当且仅当A\mathcal{A}A的特征多项式在包含FFF的代数封闭域中的全部nnn个根(重根按重数计算)都在FFF中,且对于A\mathcal{A}A的任一不变子空间WWW,都存在A\mathcal{A}A的不变子空间作为WWW在VVV中的补空间