图论中握手定理的详细解释

😄

Wilson Huang 2020/8/2

握手定理

• 前提定义1： $G=(V,E)$ 表示图 $G$ 由顶点的非空集 $V$ 和边集 $E$ 构成
• 前提定义2： 在无向图中，顶点的度是与该顶点相关联的边的数目，例外的情形是，顶点上的环为顶点的度做出了双倍的贡献。顶点 $v$ 的度表示成 $deg(v)$

设 $G=(V,E)$ 是有 $m$ 条边的无向图，则
$$2m=\sum _{v\in V}deg(v)$$
（此处注意，即使出现了多重边和环）

用通俗化的语言来表示就是：在这个图内属于这个图的每一个顶点的度的和等于这个图边的两倍

举例说明

1. 首先来看一般情况（无多重边和环）：

   

   我们可以看到这幅图有四个顶点和四条边，顶点的度分别为2,2,3,1，2+2+3+1=8=2m=2*4

2. 当出现了环：

   
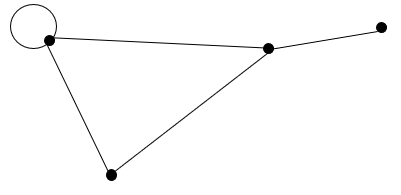
   我们可以看到这幅图比上一幅图多出了一个环，有 前提定义2 ：顶点上的环为顶点的度做出了双倍的贡献，我们可以得到，当一个顶点多了一个环，则表明这个顶点与他自己构成了一对顶点，顶点的度+2，则我们可以得出 $a$ 的度为4， $b$ 的度为2， $c$ 的度为3，$d$ 的度为1，则加起来总和为10，这幅图有5条边，所以为2m=10

3. 当出现了多重边：

   
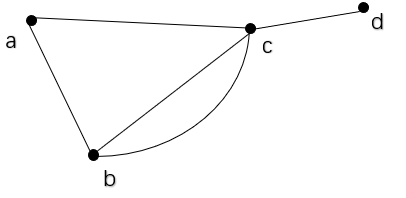
   我们可以看到这幅图有四个顶点和五条边，其中出现了一条多重边，a,b,c,d 顶点的度分别为2,3,4,1，2+3+4+1=10=2m=2*5

4. 当出现了多重边和环：

   
   我们可以看到这幅图有四个顶点和七条边，其中出现了两条条多重边和一个环，a,b,c,d 顶点的度分别为4,3,5,2，4+3+5+2=14=2m=2*7

则我们可以总结如何判断一个顶点的度：

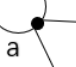
看一个顶点引出了多少条线，就证明了它的度是多少，比如a点引出了四条线，如下图所示

则a点的度为4

数学证明

在无向图 $G=(V,E)$ 中，设 $V_1$ 和 $V_2$ 分别是度为偶数的顶点和度为奇数的顶点的集合。于是：
$$2m=\sum _{v\in V}deg(v)=\sum _{v\in V_1}deg(v)+\sum _{v\in V_2}deg(v)$$

因为对 $v\in V_1$ 来说， $deg(v)$ 是偶数，所以上等式右端第一项是偶数。另外上等式右端的两项之和是偶数，因为和是 $2m$ 。因此，和里面的第二项也是偶数。因为在这个和里所有的项都是奇数，所以必然有偶数个这样的项。因此，有偶数个度为奇数的顶点。