网站有些什么内容友情链接qq群
如果周期是2π2\pi2π并且绝对可积,那么可以算傅里叶级数。
计算傅里叶级数
求之前最好说一句是按段光滑的。
1.f(x)=a02+∑(1→∞)(ancos(nx)+bnsin(nx))f(x)=\frac{a_{0}}{2}+\sum(1\to \infty)(a_{n}\cos(nx)+b_{n}\sin(nx))f(x)=2a0+∑(1→∞)(ancos(nx)+bnsin(nx))
a0=1π∫−ππf(x)dxa_{0}=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)dxa0=π1∫−ππf(x)dx
an=1π∫−ππf(x)cos(nx)dxa_{n}=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos(nx)dxan=π1∫−ππf(x)cos(nx)dx
bn=1π∫−ππf(x)sin(nx)dxb_{n}=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin(nx)dxbn=π1∫−ππf(x)sin(nx)dx
an,bn都是趋于0的
如果给的函数是0到2π2\pi2π那就算那个上面的积分。
2. 奇函数an=0,偶函数bn=0,不需要去算了
3.一般来说要用到分部积分法,把sinnxdx积出来,这个比较复杂,一定要小心。
4.cos(nπ)\cos(n\pi)cos(nπ)是(−1)n(-1)^n(−1)n,而不是1,这个要注意
傅里叶级数的收敛
收敛定理:f(x)f(x)f(x)按段光滑(在有限点不可导,其余可导)则一致收敛到了傅里叶级数。
这个证明及其烦有什么一大堆dini连续,holder连续,lip连续之类的,还有很多判别法,应该不会考。
还有一个判断傅里叶级数收敛的:就是把sincos放成1然后加绝对值的级数收敛,傅里叶级数一致收敛且绝对收敛。
计算的技巧
1.cosnx,sinnx,1在一个周期里与别人内积是0,与自己的内积是π\piπ
2.有(1-x)cosnx这种直接分布积分,无需换元
3.有关导数的这种,傅里叶级数逐项求导,方便。
周期2L的展开
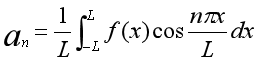
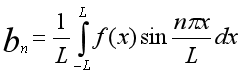
给的是0到L上的,可以奇延展或者偶延展,或者直接原模原样的延展
傅里叶级数,如果是奇偶延拓,一定换到正半周期上来算,因为负半周期的函数式都变了.
公式虽然是上面这个,但是计算时候为了方便换到正半周期上算。不然要分段积分了。
如果是偶函数可以算0到L的2倍
