海口网约车需要什么条件长沙优化排名推广

题目：

利用最优二叉搜索树来实现树的搜索代价最小。树上的每一个节点都有一个被搜索到的概率值pipi，搜索一个节点的花费为pi∗（depth(ki)+1）pi∗（depth(ki)+1），如何构造一个二叉查找树使搜索树上的 所有节点的花费最小即为实现最优二叉查找树的问题。该问题可以用动态规划的思路实现。 
　　形式化定义：给定n个不同关键字已经排序的序列K=(k1,k2,...,kn)因此(k1<k2<k3<...<kn)K=(k1,k2,...,kn)因此(k1<k2<k3<...<kn),我们希望用这些关键字构造一个二叉搜索树。对每个关键字kiki,都有概率pipi表示起搜索概率。有些要搜索的值可能不再K中，因此我们还需要n+1个伪关键字(d0,d1,d2,...dn)(d0,d1,d2,...dn)，对于每一个伪关键字都有一个概率qiqi表示对应的搜索概率。

输入输出：

输入为：结点的个数n，搜索成功的概率bi，搜索失败的概率aj。以作业为例；

输出为：最优二叉树的结构。

源代码：

/*
最优搜索二叉树
*/
#include<iostream>
#include<stdio.h>
using namespace std;
#define MAX 30int n;//搜索元素个数
int b[MAX];//n个节点的对应的概率
int a[MAX + 1];//处在n个节点中间那些不存在的n+1虚节点
int w[MAX][MAX], m[MAX][MAX], s[MAX][MAX];void input()
{cout << "请输入节点的数目:" << endl;cin >> n;cout << "请输入" << n << "个节点搜索成功的概率:" << endl;for (int i = 1; i <= n; i++)cin >> b[i];cout << "请输入" << n + 1 << "个虚节点节点搜索成功的概率:" << endl;for (int i = 0; i <= n; i++)cin >> a[i];}void OBST()
{for (int i = 0; i <= n; i++){w[i + 1][i] = a[i];m[i + 1][i] = 0;s[i + 1][i] = 0;}for (int r = 0; r<n; r++){for (int i = 1; i <= n - r; i++){int j = i + r;w[i][j] = w[i][j - 1] + a[j] + b[j];m[i][j] = m[i + 1][j];s[i][j] = i;for (int k = i + 1; k <= j; k++){int t = m[i][k - 1] + m[k + 1][j];if (t < m[i][j]){m[i][j] = t;s[i][j] = k;}}m[i][j] += w[i][j];}}
}void Tree_Struct(int i, int j)
{if (i<j){int root = s[i][j];printf("D%d 是根\n", root);if (s[i][root - 1]>0){printf("D%d 的左孩子是 D%d\n", root, s[i][root - 1]);}if (s[root + 1][j]>0){printf("D%d 的右孩子是 D%d\n", root, s[root + 1][j]);}Tree_Struct(i, root - 1);Tree_Struct(root + 1, j);}
}
void print_s()
{cout<<"最优子树的根节点矩阵:"<<endl;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cout<<s[i][j]<<" ";}cout<<endl;}
}
int main()
{input();OBST();print_s();Tree_Struct(1, n);system("pause");return 0;
}

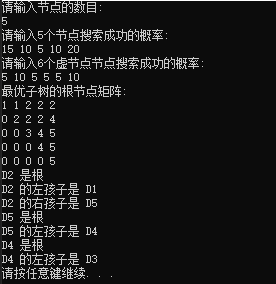
 实验结果：