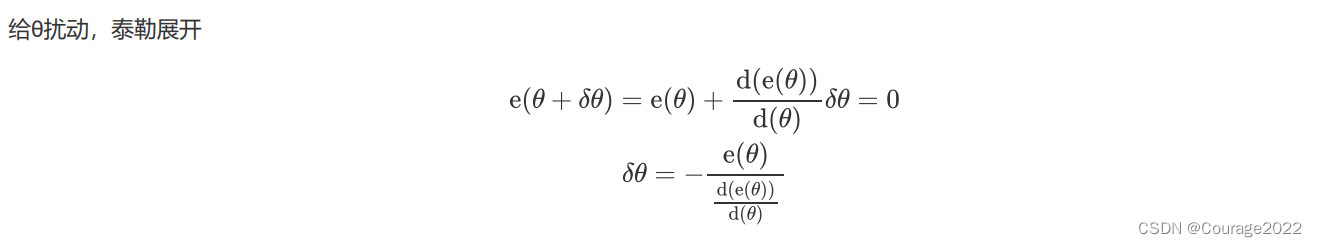当前位置：首页 > news >正文

网站开发架构/嘉兴seo外包

news 2025/8/16 2:15:03

网站开发架构,嘉兴seo外包,国内知名的网站建设公司,做义工旅行有哪些网站目录 1.相机基类GeometricCamera.h 1.1 GeometricCamera类 2.针孔相机模型 Pinhole 2.1 Pinhole.h 2.2 Pinhole.cpp实现函数 2.2.1 投影函数 2.2.2 反投影函数 2.2.3 恢复三维点 3.鱼眼相机模型 3.1 鱼眼相机投影的数学基础KannalaBrandt8::project 3.2 鱼眼相机反投影…

1.相机基类GeometricCamera.h

1.1 GeometricCamera类

2.针孔相机模型 Pinhole

2.1 Pinhole.h

2.2 Pinhole.cpp实现函数

2.2.1 投影函数

2.2.2 反投影函数

2.2.3 恢复三维点

3.鱼眼相机模型

3.1 鱼眼相机投影的数学基础KannalaBrandt8::project

3.2 鱼眼相机反投影的数学基础

1.相机基类GeometricCamera.h

1.1 GeometricCamera类

是一个纯虚类，无法实例化对象，只能通过继承来实现。

从C++的角度来讲，判断一个类是否是纯虚类只需要看后面的虚函数是否有=0的部分：

virtual cv::Point2f project(const cv::Point3f &p3D) = 0;

纯虚类无法实例化，只能通过继承来实现。纯虚函数也是没有办法直接实现的，需要通过在继承类重写才能使用。

namespace ORB_SLAM3 {class GeometricCamera {friend class boost::serialization::access;template<class Archive>void serialize(Archive& ar, const unsigned int version){ar & mnId;ar & mnType;ar & mvParameters;}public:GeometricCamera() {}GeometricCamera(const std::vector<float> &_vParameters) : mvParameters(_vParameters) {}~GeometricCamera() {}// 投影函数 输入:相机坐标下的三维点 输出:图片上的像素坐标 好多重载函数应用于不同类型virtual cv::Point2f project(const cv::Point3f &p3D) = 0;virtual Eigen::Vector2d project(const Eigen::Vector3d & v3D) = 0;virtual Eigen::Vector2f project(const Eigen::Vector3f & v3D) = 0;virtual Eigen::Vector2f projectMat(const cv::Point3f& p3D) = 0;// 返回像素点的不确定性 不管输入是什么 返回都是1.0f的float类型virtual float uncertainty2(const Eigen::Matrix<double,2,1> &p2D) = 0;// 反投影 输入的是一个像素点的坐标 输出的是在相机坐标系下归一化平面的坐标 反投影没有尺度因此深度无法求得virtual Eigen::Vector3f unprojectEig(const cv::Point2f &p2D) = 0;virtual cv::Point3f unproject(const cv::Point2f &p2D) = 0;virtual Eigen::Matrix<double,2,3> projectJac(const Eigen::Vector3d& v3D) = 0;// 三角化恢复三维点 主要在单目初始化的时候调用virtual bool ReconstructWithTwoViews(const std::vector<cv::KeyPoint>& vKeys1, const std::vector<cv::KeyPoint>& vKeys2, const std::vector<int> &vMatches12,Sophus::SE3f &T21, std::vector<cv::Point3f> &vP3D, std::vector<bool> &vbTriangulated) = 0;//返回 K 矩阵 3*3virtual cv::Mat toK() = 0;virtual Eigen::Matrix3f toK_() = 0;// 极线约束 三角化MP使用virtual bool epipolarConstrain(GeometricCamera* otherCamera, const cv::KeyPoint& kp1, const cv::KeyPoint& kp2, const Eigen::Matrix3f& R12, const Eigen::Vector3f& t12, const float sigmaLevel, const float unc) = 0;// 设置和获取相机的内参数float getParameter(const int i){return mvParameters[i];}void setParameter(const float p, const size_t i){mvParameters[i] = p;}size_t size(){return mvParameters.size();}virtual bool matchAndtriangulate(const cv::KeyPoint& kp1, const cv::KeyPoint& kp2, GeometricCamera* pOther,Sophus::SE3f& Tcw1, Sophus::SE3f& Tcw2,const float sigmaLevel1, const float sigmaLevel2,Eigen::Vector3f& x3Dtriangulated) = 0;unsigned int GetId() { return mnId; }unsigned int GetType() { return mnType; }// 针孔是0,鱼眼是1const static unsigned int CAM_PINHOLE = 0;const static unsigned int CAM_FISHEYE = 1;static long unsigned int nNextId;protected:// 存放参数 包括K的参数和畸变std::vector<float> mvParameters;unsigned int mnId;unsigned int mnType;};
}

2.针孔相机模型 Pinhole

2.1 Pinhole.h

针孔相机模型继承于相机基类GeometricCamera：

namespace ORB_SLAM3 {// 针孔类模型 继承自相机基类class Pinhole : public GeometricCamera {friend class boost::serialization::access;template<class Archive>void serialize(Archive& ar, const unsigned int version){ar & boost::serialization::base_object<GeometricCamera>(*this);}public:Pinhole() {// 参数只有四个 fx fy cx cy,没有关于畸变的参数,也就是说针孔模型已经把所有的点给去畸变化了,到相机这块的时候已经是去畸变后的点了mvParameters.resize(4);mnId=nNextId++;mnType = CAM_PINHOLE;}// _vParameters相机内参Pinhole(const std::vector<float> _vParameters) : GeometricCamera(_vParameters), tvr(nullptr) {// fx fy cx cy 并没有畸变...也就是说针孔模型下 已经将所有的像素点去畸变化了 到相机后所有的点已经是去畸变后的了 没有保存有关畸变的数据assert(mvParameters.size() == 4);mnId=nNextId++;mnType = CAM_PINHOLE;}Pinhole(Pinhole* pPinhole) : GeometricCamera(pPinhole->mvParameters), tvr(nullptr) {assert(mvParameters.size() == 4);mnId=nNextId++;mnType = CAM_PINHOLE;}~Pinhole(){if(tvr) delete tvr;}// 投影函数cv::Point2f project(const cv::Point3f &p3D);Eigen::Vector2d project(const Eigen::Vector3d & v3D);Eigen::Vector2f project(const Eigen::Vector3f & v3D);Eigen::Vector2f projectMat(const cv::Point3f& p3D);// 返回像素点的不确定性 不管是啥都返回1.0ffloat uncertainty2(const Eigen::Matrix<double,2,1> &p2D);//反投影 2D -> 3D 深度为1的相机坐标系Eigen::Vector3f unprojectEig(const cv::Point2f &p2D);cv::Point3f unproject(const cv::Point2f &p2D);Eigen::Matrix<double,2,3> projectJac(const Eigen::Vector3d& v3D);bool ReconstructWithTwoViews(const std::vector<cv::KeyPoint>& vKeys1, const std::vector<cv::KeyPoint>& vKeys2, const std::vector<int> &vMatches12,Sophus::SE3f &T21, std::vector<cv::Point3f> &vP3D, std::vector<bool> &vbTriangulated);cv::Mat toK();Eigen::Matrix3f toK_();bool epipolarConstrain(GeometricCamera* pCamera2, const cv::KeyPoint& kp1, const cv::KeyPoint& kp2, const Eigen::Matrix3f& R12, const Eigen::Vector3f& t12, const float sigmaLevel, const float unc);bool matchAndtriangulate(const cv::KeyPoint& kp1, const cv::KeyPoint& kp2, GeometricCamera* pOther,Sophus::SE3f& Tcw1, Sophus::SE3f& Tcw2,const float sigmaLevel1, const float sigmaLevel2,Eigen::Vector3f& x3Dtriangulated) { return false;}friend std::ostream& operator<<(std::ostream& os, const Pinhole& ph);friend std::istream& operator>>(std::istream& os, Pinhole& ph);bool IsEqual(GeometricCamera* pCam);private:// 两帧恢复三维点,两帧重建//Parameters vector corresponds to//      [fx, fy, cx, cy]TwoViewReconstruction* tvr;};
}

2.2 Pinhole.cpp实现函数

2.2.1 投影函数

/** * @brief 相机坐标系下的三维点投影到无畸变像素平面* @param v3D 三维点* @return 像素坐标*/
Eigen::Vector2d Pinhole::project(const Eigen::Vector3d &v3D)
{Eigen::Vector2d res;// u = fx * x/z + cx// v = fy * y/z + cy// mvParameters = [fx,fy,cx,cy]res[0] = mvParameters[0] * v3D[0] / v3D[2] + mvParameters[2];res[1] = mvParameters[1] * v3D[1] / v3D[2] + mvParameters[3];return res;
}

mvParameters存放着相机内参 $f_x,f_y,c_x,c_y$ 。通过如下方式投影：

$\begin{bmatrix} u\\ v \end{bmatrix} = K\cdot \begin{bmatrix} X\\ Y \\ Z \end{bmatrix} = \begin{bmatrix} f_x & 0 &c_x \\ x& f_y &c_y \\ 0 &0 &1 \end{bmatrix} \begin{bmatrix} X\\ Y\\ Z \end{bmatrix}$

2.2.2 反投影函数

/** * @brief 反投影* @param p2D 特征点* @return 归一化坐标*/
cv::Point3f Pinhole::unproject(const cv::Point2f &p2D)
{return cv::Point3f((p2D.x - mvParameters[2]) / mvParameters[0],(p2D.y - mvParameters[3]) / mvParameters[1],1.f);
}
        由公式：

$u = f_x \frac{X}{Z} +c_x$

$v = f_y \frac{Y}{Z} +c_y$

        分离出 $X,Y$ 有：

$X =\frac{Z(u-c_x)}{f_x}$

$Y =\frac{Z(v-c_y)}{f_y}$

        又由于像素坐标系没有尺度信息，因此我们令 $Z$ 为1。得到归一化平面的三维坐标。

2.2.3 恢复三维点

TwoViewReconstruction::TwoViewReconstruction(const Eigen::Matrix3f &k, float sigma, int iterations)
{mK = k;mSigma = sigma;mSigma2 = sigma * sigma;mMaxIterations = iterations;
}

其实有用的部分就是把相机的内参拷贝进去了。

/** 三角化恢复三维点  单目初始化时使用* @param vKeys1 第一帧的关键点* @param vKeys2 第二帧的关键点* @param vMatches12 匹配关系，长度与vKeys1一样，对应位置存放vKeys2中关键点的下标* @param R21 顾名思义* @param t21 顾名思义* @param vP3D 恢复出的三维点* @param vbTriangulated 是否三角化成功，用于统计匹配点数量*/
bool Pinhole::ReconstructWithTwoViews(const std::vector<cv::KeyPoint> &vKeys1, const std::vector<cv::KeyPoint> &vKeys2, const std::vector<int> &vMatches12,Sophus::SE3f &T21, std::vector<cv::Point3f> &vP3D, std::vector<bool> &vbTriangulated)
{if (!tvr){// 用内参K构造 TwoViewReconstruction类Eigen::Matrix3f K = this->toK_();tvr = new TwoViewReconstruction(K);}// 返回 两帧之间的变换矩阵T21 和成功的三角化的点vP3D 以及是否三角化成功的标志vbTriangulatedreturn tvr->Reconstruct(vKeys1, vKeys2, vMatches12, T21, vP3D, vbTriangulated);
}

3.鱼眼相机模型

3.1 鱼眼相机投影的数学基础KannalaBrandt8::project

鱼眼相机和普通相机相比，有更大的观测空间，在针孔相机模型中，只需要利用相似三角形原理就可以实现由三维点向二维点的投影。

如图， $x_c$ 是归一化平面的相对于相机坐标的 $x$ 偏移量， $f$ 是相机的焦距。

因此，通过这俩相似三角形就可以得到在像素平面的坐标。

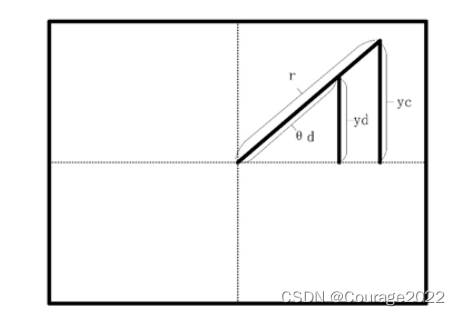
在鱼眼相机模型中，我们无法通过相似三角形的方式得到像素坐标，下面我们来介绍如何获得像素坐标，下面我们先了解图中各变量的意义：

         $f$ ：焦距

         $\theta$ ：观测到的归一化平面的三维点与相机的夹角

         $\theta ^\cdot$ ：处理后的夹角

下面推导过程：带c下标的表示畸变前的，带d下标的表示畸变后的。

计算归一化坐标：

$x_c =\frac{X_c}{Z_c},y_c=\frac{Y_c}{Z_c}$

计算 $r$ 和 $\theta$ ：

$r^2 = x_c^2+y_c^2,\theta =arctan(r)$

计算 $\theta _d$ ：

$\theta _d = k_0\theta + k_1\theta^3+k_2\theta^5 + k_3\theta^7+k_4\theta^9$

计算去畸变后的归一化平面坐标：

$x_d = \frac{\theta_d}{r}\cdot x_c,y_d = \frac{\theta_d}{r}\cdot y_c$

最后计算像素点：

$u=f_x \cdot x_d+c_x,v=f_y\cdot y_d+c_y$

至此，我们就得到了三维点在像素坐标系上的投影。
/** * @brief 投影* xc = Xc/Zc, yc = Yc/Zc* r^2 = xc^2 + yc^2* θ = arctan(r)* θd = k0*θ + k1*θ^3 + k2*θ^5 + k3*θ^7 + k4*θ^9* xd = θd/r * xc   yd = θd/r * yc* u = fx*xd + cx  v = fy*yd + cy* @param p3D 三维点* @return 像素坐标*/
cv::Point2f KannalaBrandt8::project(const cv::Point3f &p3D)
{const float x2_plus_y2 = p3D.x * p3D.x + p3D.y * p3D.y;const float theta = atan2f(sqrtf(x2_plus_y2), p3D.z);const float psi = atan2f(p3D.y, p3D.x);const float theta2 = theta * theta;const float theta3 = theta * theta2;const float theta5 = theta3 * theta2;const float theta7 = theta5 * theta2;const float theta9 = theta7 * theta2;const float r = theta + mvParameters[4] * theta3 + mvParameters[5] * theta5 + mvParameters[6] * theta7 + mvParameters[7] * theta9;return cv::Point2f(mvParameters[0] * r * cos(psi) + mvParameters[2],mvParameters[1] * r * sin(psi) + mvParameters[3]);
}

3.2 鱼眼相机反投影的数学基础

主要是一个计算与迭代的过程。

/** * @brief 反投影* 投影过程* xc = Xc/Zc, yc = Yc/Zc* r^2 = xc^2 + yc^2* θ = arctan(r)* θd = k0*θ + k1*θ^3 + k2*θ^5 + k3*θ^7 + k4*θ^9* xd = θd/r * xc   yd = θd/r * yc* u = fx*xd + cx  v = fy*yd + cy* * * 已知u与v 未矫正的特征点像素坐标* xd = (u - cx) / fx    yd = (v - cy) / fy* 待求的 xc = xd * r / θd  yc = yd * r / θd* 待求的 xc = xd * tan(θ) / θd  yc = yd * tan(θ) / θd* 其中 θd的算法如下：*     xd^2 + yd^2 = θd^2/r^2 * (xc^2 + yc^2)*     θd = sqrt(xd^2 + yd^2) / sqrt(xc^2 + yc^2) * r*     其中r = sqrt(xc^2 + yc^2)*     所以 θd = sqrt(xd^2 + yd^2)  已知* 所以待求的只有tan(θ),也就是θ* 这里θd = θ + k1*θ^3 + k2*θ^5 + k3*θ^7 + k4*θ^9* 直接求解θ比较麻烦，这里用迭代的方式通过误差的一阶导数求θ* θ的初始值定为了θd，设θ + k1*θ^3 + k2*θ^5 + k3*θ^7 + k4*θ^9 = f(θ)* e(θ) = f(θ) - θd 目标是求解一个θ值另e(θ) = 0* 泰勒展开e(θ+δθ) = e(θ) + e`(θ) * δθ = 0* e`(θ) = 1 + 3*k1*θ^*2 + 5*k2*θ^4 + 7*k3*θ^6 + 8*k4*θ^8* δθ = -e(θ)/e`(θ) 经过多次迭代可求得θ* 最后xc = xd * tan(θ) / θd  yc = yd * tan(θ) / θd* @param p2D 特征点* @return */
cv::Point3f KannalaBrandt8::unproject(const cv::Point2f &p2D)
{// Use Newthon method to solve for theta with good precision (err ~ e-6)cv::Point2f pw((p2D.x - mvParameters[2]) / mvParameters[0], (p2D.y - mvParameters[3]) / mvParameters[1]);float scale = 1.f;float theta_d = sqrtf(pw.x * pw.x + pw.y * pw.y);  // sin(psi) = yc / rtheta_d = fminf(fmaxf(-CV_PI / 2.f, theta_d), CV_PI / 2.f);  // 不能超过180度if (theta_d > 1e-8){// Compensate distortion iteratively// θ的初始值定为了θdfloat theta = theta_d;// 开始迭代for (int j = 0; j < 10; j++){float theta2 = theta * theta,theta4 = theta2 * theta2,theta6 = theta4 * theta2,theta8 = theta4 * theta4;float k0_theta2 = mvParameters[4] * theta2,k1_theta4 = mvParameters[5] * theta4;float k2_theta6 = mvParameters[6] * theta6,k3_theta8 = mvParameters[7] * theta8;float theta_fix = (theta * (1 + k0_theta2 + k1_theta4 + k2_theta6 + k3_theta8) - theta_d) /(1 + 3 * k0_theta2 + 5 * k1_theta4 + 7 * k2_theta6 + 9 * k3_theta8);theta = theta - theta_fix;if (fabsf(theta_fix) < precision)  // 如果更新量变得很小，表示接近最终值break;}// scale = theta - theta_d;// 求得tan(θ) / θdscale = std::tan(theta) / theta_d;}return cv::Point3f(pw.x * scale, pw.y * scale, 1.f);
}

查看全文

http://www.lbrq.cn/news/1566811.html