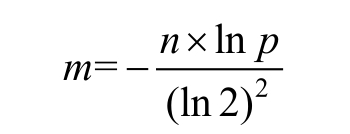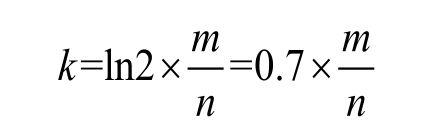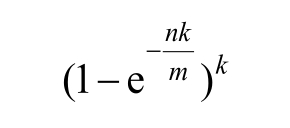布隆过滤器

• BloomFilter 的目的是检测一个元素是否存在于一个集合内。
• 本质上布隆过滤器是一种数据结构，比较巧妙的概率型数据结构，特点是高效地插入和查询。根据查询结果可以用来告诉你 某样东西一定不存在或者可能存在 这句话是该算法的核心。
• 相比于传统的 List、Set、Map 等数据结构，它更高效、占用空间更少，但是缺点是其返回的结果是概率性的，而不是确切的，同时布隆过滤器还有一个缺陷就是数据只能插入不能删除。

【题目】和【要求】

不安全网页的黑名单包含100亿个黑名单网页，每个网页的URL最多占用64B。现在想要实现一个网页过滤系统，利用该系统可以根据网页的URL判断该网页是否在黑名单上，请设计该系统。

1. 该系统允许有万分之一以下的判断失误率。
2. 使用的额外空间不要超过30GB。

首先介绍哈希函数（散列函数）的概念

• 哈希函数的输入域可以是非常大的范围，比如，任意一个字符串，但是输出域是固定的范围，假设为S，并具有如下性质：

1. 典型的哈希函数都有无限的输入值域。
2. 当给哈希函数传入相同的输入值时，返回值一样。
3. 当给哈希函数传入不同的输入值时，返回值可能一样，也可能不一样，这是当然的。因为输出域统一是S，所以会有不同的输入值对应在S中的一个元素上。
4. 最重要的性质是很多不同的输入值所得到的返回值会均匀地分布在S上。

• 第1～3点性质是哈希函数的基础。
• 第4点性质是评价一个哈希函数优劣的关键。
• 不同的输入值所得到的返回值越均匀地分布在S上，哈希函数就越优秀，并且这种均匀分布与输入值出现的规律无关。

• 如果一个优秀的哈希函数能够做到很多不同的输入值所得到的返回值非常均匀地分布在S上，那么将所有的返回值对m取余（%m），可以认为所有的返回值也会均匀地分布在0～m-1的空间上。

接下来介绍一下什么是布隆过滤器。

• 假设有一个长度为m的bit类型的数组，即数组中的每一个位置只占一个bit，如我们所知，每一个bit只有0和1两种状态。 如图下图所示。

• 再假设一共有k个哈希函数，这些函数的输出域S都大于或等于m，并且这些哈希函数都足够优秀，彼此之间也完全独立。那么对同一个输入对象（假设是一个字符串，记为URL），经过 k个哈希函数算出来的结果也是独立的，可能相同，也可能不同，但彼此独立。对算出来的每一个结果都对m取余（%m），然后在bit array上把相应的位置设置为1（涂黑），如图下图所示。
  

• 我们把bit类型的数组记为bitMap。

• 至此，一个输入对象对bitMap的影响过程就结束了，也就是bitMap中的一些位置会被涂黑。

• 接下来按照该方法处理所有的输入对象，每个对象都可能把bitMap中的一些白位置涂黑，也可能遇到已经涂黑的位置，遇到已经涂黑的位置让其继续为黑即可。

• 处理完所有的输入对象后，可能bitMap中已经有相当多的位置被涂黑。

• 至此，一个布隆过滤器生成完毕，这个布隆过滤器代表之前所有输入对象组成的集合。
  

那么在检查阶段如何检查某一个对象是否是之前的某一个输入对象呢？

• 假设一个对象为a，想检查它是否是之前的输入对象，就把a通过k个哈希函数算出k个值，然后把k个值取余（%m），就得到在[0，m-1]范围上的k个值。接下来在bitMap上看这些位置是不是都为黑。
• 如果有一个不为黑，说明a一定不在这个集合里。
• 如果都为黑，说明a在这个集合里，但可能有误判。
• 再解释具体一点，如果a的确是输入对象，那么在生成布隆过滤器时，bitMap中相应的k个位置一定已经涂黑了，所以在检查阶段，a一定不会被漏过，这个不会产生误判。
• 会产生误判的是，a明明不是输入对象，但如果在生成布隆过滤器的阶段因为输入对象过多，而bitMap过小，则会导致bitMap绝大多数的位置都已经变黑。那么在检查a时，可能a对应的k个位置都是黑的，从而错误地认为a是输入对象。
• 通俗地说，布隆过滤器的失误类型是“宁可错杀三千，绝不放过一个”。

布隆过滤器到底该怎么实现？

• 如果 bitMap的大小 m相比输入对象的个数n过小，失误率会变大。
• 接下来先介绍根据n的大小和我们想达到的失误率p，如何确定布隆过滤器的大小m和哈希函数的个数k，最后是布隆过滤器的失误率分析。下面以本题为例来说明。

• 黑名单中样本的个数为100亿个，记为n；失误率不能超过0.01%，记为p；
• 每个样本的大小为 64B，这个信息不会影响布隆过滤器的大小，只和选择哈希函数有关，一般的哈希函数都可以接收64B的输入对象，所以使用布隆过滤器还有一个好处是不用顾忌单个样本的大小，它丝毫不能影响布隆过滤器的大小。
• 所以n=100亿，p=0.01%，布隆过滤器的大小m由以下公式确定：
  
• 根据公式计算出m=19.19n，向上取整为20n，即需要2000亿个bit，也就是25GB。

哈希函数的个数由以下公式决定：

• 计算出哈希函数的个数为k=14个。
• 然后用25GB的bitMap再单独实现14个哈希函数，根据如上描述生成布隆过滤器即可。
• 因为我们在确定布隆过滤器大小的过程中选择了向上取整，所以还要用如下公式确定布隆过滤器真实的失误率为:
  
• 根据这个公式算出真实的失误率为0.006%，这是比0.01%更低的失误率，哈希函数本身不占用什么空间，所以使用的空间就是bitMap的大小（即25GB），服务器的内存都可以达到这个级别，所有要求达标。

• 布隆过滤器会有误报，对已经发现的误报样本可以通过建立白名单来防止误报。
• 比如，已经发现“aaaaaa5”这个样本不在布隆过滤器中，但是每次计算后的结果都显示其在布隆过滤器中，那么就可以把这个样本加入白名单中，以后就可以知道这个样本确实不在布隆过滤器中。

使用场景

• 网页爬虫对URL的去重，避免爬去相同的URL地址。
• 垃圾邮件过滤，从数十亿个垃圾邮件列表中判断某邮箱是否是杀垃圾邮箱。
• 解决数据库缓存击穿，黑客攻击服务器时，会构建大量不存在于缓存中的key向服务器发起请求，在数据量足够大的时候，频繁的数据库查询会导致挂机。
• 秒杀系统，查看用户是否重复购买。

参考资料：

• 《程序员代码面试指南》