做项目接任务的网站/网络营销怎么做推广

这是xgboost原论文的伪代码介绍，可以看到实际上就是对缺失值的处理，现在没有缺失的值上分裂，然后把缺失值分别带入左节点算一下分裂后的增益，再带入右节点算一下分裂后的增益然后去其中大的一个作为最终的分裂方案。如果训练中没有数据缺失，预测时出现了数据缺失，则默认被分类到右节点，原作者在这里是把缺失值描述为稀疏矩阵引起了歧义，实际上很我们常规意义上理解的那种onehot之后一大堆0的情况不一样，lightgbm的efb特征捆绑才是真正对这种0很多的特征进行合并从而实现稀疏特征的优化。

这里做个实验：

import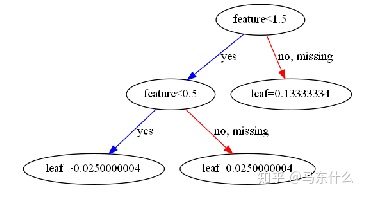 

可以看到，0是当作一个正常的值来对待的而不是当作缺失值对待的。

如果我们要处理非常稀疏的特征，比如一列特征有90%的值都是0，并且这些0值的含义值都是缺失值，那么我们可以直接将0替换为np.nan，或者将xgb中的参数missing设置为0（如果设置为0则xgboost就无法处理np.nan的缺失值了，运行的时候如果原特征中存在np.nan会报错）。

不过这篇文章给出了一个新的发现很有意思。如果我们把原始数据按照稀疏矩阵的方式进行压缩存储。

from scipy.sparse import csr_matrix
d=pd.DataFrame()
d['feature']=[0,1,2,np.nan]
y=pd.DataFrame([0,1,2,3])
d=csr_matrix(d)
clf.fit(d,y)
xgb.plot_tree(clf)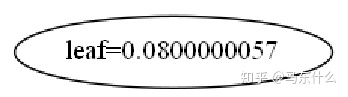

这样就只得到一个单节点了。为了比较又做了一组实验

d=pd.DataFrame()
d['feature']=[1,1,2,np.nan]
y=pd.DataFrame([1,1,2,3])
clf.fit(d,y)
xgb.plot_tree(clf)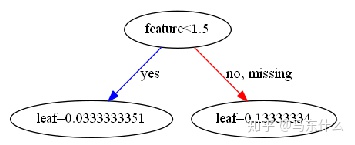

d=pd.DataFrame()
d['feature']=[1,1,2,np.nan]
y=pd.DataFrame([1,1,2,3])
d=csr_matrix(d)
clf.fit(d,y)
xgb.plot_tree(clf)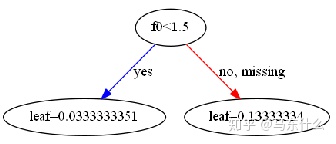

可以看到如果原始特征中没有0，进行矩阵压缩之后结果是一样的，如果原始特征中存在0，则矩阵压缩之后结果不一样，

所以，xgboost对于稀疏矩阵压缩之后的处理就是把0和np.nan都统一当作了缺失值。我想所谓的优化就是在这里。显然这是一个很不好的设置，因为如果原始特征中的0是有意义的，那么这样处理显然破坏了原始特征，所以上面链接里的作者提到建议用稠密矩阵而不是压缩之后的矩阵进行训练。不过其实问题不大，我们只需要对有意义的0值赋一个0.0000000000001的值就可以解决这个问题了，而且矩阵压缩之后内存占用非常小，训练要比原来快很多。