目录

前言

二叉树的基本基本操作

获取树中节点的个数

获取叶子节点的个数 

 获取第K层节点的个数

获取二叉树的高度 

检测值为val的元素是否存在 

判断一棵树是不是完全二叉树 

---

前言

二叉树的基本基本操作

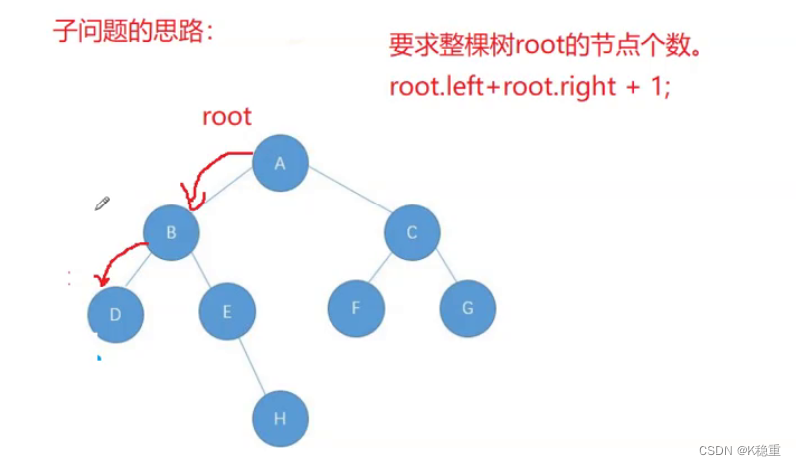
获取树中节点的个数

遍历思路代码:

//获取树中节点的个数
int count = 0;
public int size1(BTNode root){if(root == null) {return 0;}count ++;count += size1(root.left);count += size1(root.right);return count;
}

子问题思路:

//子问题思路
public int size2(BTNode root){if (root == null){return 0;}return size2(root.left) + size2(root.right) + 1;
}

获取叶子节点的个数 

遍历思路:

遍历到叶子节点,就让计数器++

叶子节点:root.left == null && root.right == null

public int leafNodes(BTNode root){int count = 0;if(root == null){return 0;}if(root.left == null && root.right == null){count++;}leafNodes(root.left);leafNodes(root.right);return count;}

子问题思路:

左树叶子节点加右树叶子节点

public int leafNodes(BTNode root){if(root == null){return 0;}if(root.left == null && root.right == null){return 1;}return leafNodes(root.left) + leafNodes(root.right);
}

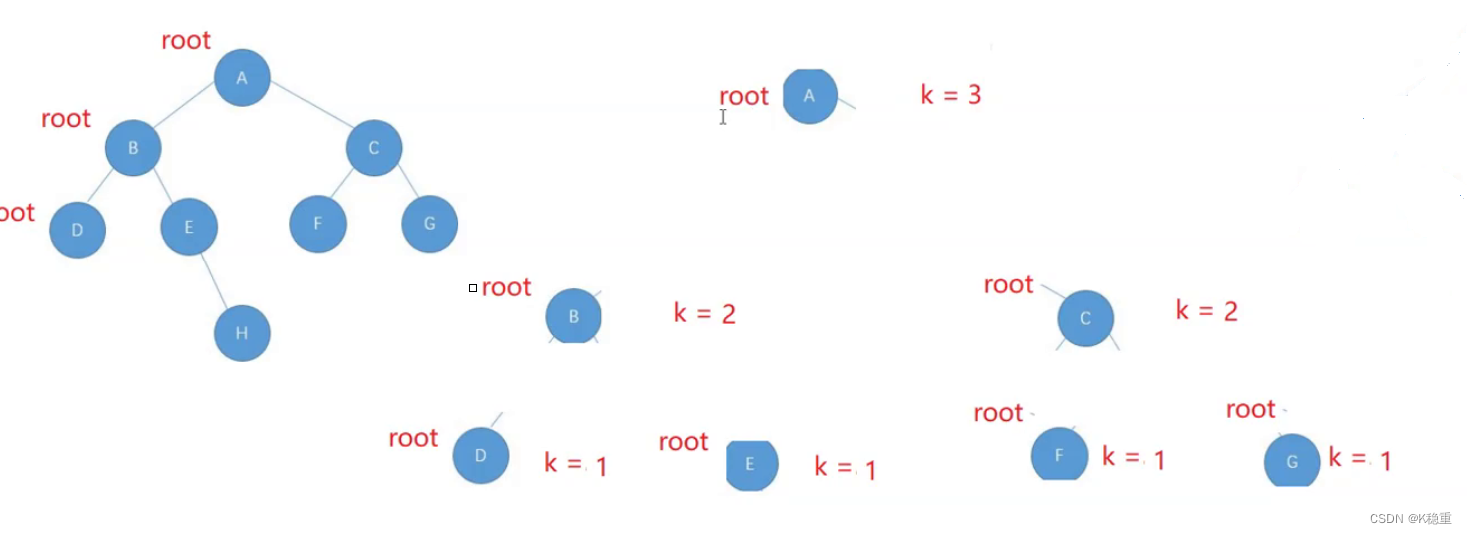
 获取第K层节点的个数

假设K等于3

也就是A的第三层

B,C的第二层

D,E,F,G的第一层

终止条件K等于1

public int getKLeveLNodeCount(BTNode root, int k){if(root == null || k <= 0){return 0;}if(k == 1){return 1;}return getKLeveLNodeCount(root.left,k - 1) + getKLeveLNodeCount(root.right ,k-1);}

获取二叉树的高度 

子问题思路

左树的高度和右树的高度取最大值,然后加1 = 整棵树的高度

public int getHeight(BTNode root){if(root == null){return 0;}int leftHeight = getHeight(root.left);int rightHeight = getHeight(root.right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;

检测值为val的元素是否存在 

 public BTNode find(BTNode root,char val){if(root == null){return null;}if(root.val == val){return root;}BTNode ret = find(root.left,val);if(ret != null){return ret;}ret = find(root.right,val);if(ret != null){return ret;}
return null;}

判断一棵树是不是完全二叉树 

public boolean getHeight3(BTNode root){if (root == null) return true;Queue<BTNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()){BTNode cur = queue.poll();if (cur != null){queue.offer(cur.left);queue.offer(cur.right);}else {break;}}while (!queue.isEmpty()){BTNode ret = queue.peek();if(ret != null){return false;}queue.poll();}
return true;}