如何做360搜索网站/产品推广平台

费马小定理

对于一个质数p,任意的整数a（a不是p的倍数），都有：

a^（p-1）≡1（mod p）

证明此定理，我们首先需要证明一下欧拉定理。

欧拉定理：

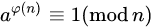
对于互质的两个数a和n,有：

我们设n的简化剩余系（ 本 质是比 n 小且与 n 互质的数）为：b1,b2,b3…bφ(n)。

这里，我们会用到反证法：假设i ! = j,a * b[i] ≡ a * b[j] (mod n) , 因为a与n互质，所以：b[i]≡b[j] (mod n)。但是，我们知道，b[i]显然不与b[j]在模n的情况下同余。所以，

a * b[i] ≡ a * b[j] (mod n)显然不成立。

所以，当一个与n互质的数与b[1]~b[φ(n)]依次相乘，每次得到的数再%n后，得到的数都不一样，

且得到的数都属于b[1]~b[n]区间，这便是乘法封闭。

所以，便得出以下式子：

• $a^{\phi (n)}$ * ( b1 * b2 * b3 ……bφ(n)) ≡ b1 * b2 * b3 ……bφ(n)(mod n)

所以： $a^{\phi (n)}$ ≡ 1 (mod n)。

当n为质数时，φ(n)=n-1,这便与费马小定理不期而遇了：$a^{p-1}$ ≡1（mod p）

此处，我们将会涉及到逆元的定义： 比如，对于a与p两个数，有一个数x，使得a * x ≡ 1 (mod p)，那么，我们就称x为mod p意义下a的逆元

又因为a与p互质，所以： x ≡ $\frac{1}{a}$ (mod p)。

由费马小定理可得，$ a^{p-2} $\equiv$ \frac{1}{a}$ (mod p)。那么，我们就可以求得a在mod p意义下的逆元了。

费马小定理的用处，就是用在有关组合数学的题目上，因为有关组合的题目，输出值一般都会比较大，这时，题目就会给你一个较大的质数 ，然后让你输出答案mod上这个质数。我们也都知道，组合数学，一般都要用上除法，我们再将除法转化为同余，就能很轻松地解决相应的问题了。

此处，奉上我码的一个相应的板子（很青涩，但比较简洁）。

求逆元：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=20001000;
ll n,p;
ll f[N],ni[N],ci[N];//jie存阶层，ni存逆元，ci存P-2次方； 
ll fang(ll a,ll b)
{ll sum=1;while(b){a%=p;sum%=p;if(b&1) sum=(sum%p*(a%p))%p;b=b>>1;a=(a%p*(a%p))%p;}return sum%p;
}
int main()
{scanf("%d%d",&n,&p);f[0]=1;f[1]=1;for(ll i=2;i<=n;i++) f[i]=(f[i-1]*i)%p;ci[n]=fang(f[n],p-2);for(ll i=n-1;i>=1;i--)ci[i]=(ci[i+1]*(i+1))%p;for(ll i=1;i<=n;i++){ni[i]=(ci[i]*f[i-1])%p;}for(ll i=1;i<=n;i++)printf("%lld\n",ni[i]);return 0;
}