科学计数法

规格化的数，小数点前一位不为0
如：$1.23\times 10^4$
解析一下这个式子，1.23是尾数，10是基，4是指数（阶码）
相应的，二进制同样道理
如：$1.101\times 2^{1111}$
1.101是尾数，2是基，1111是指数
因此对尾数和指数分别编码即可表示一个浮点数（基已经规定，无需表示）

浮点数的表示

第一位是符号位，0为正，1为负。
2至9位用移码表示阶码，偏置常数是2^7=128。
10至32位用原码表示尾数，规格化的尾数首位不是0，所以尾数的第一位一定是1，所以规定不用显式的表示1，所以10至32位共23位数，可以表示24位数（尾数首位1省略）

表示范围

小数点在1前
最大的正数：$0.111\dots 11\times 2^{11...11}=(1-2^{-24})\times 2^{256-1-128}=(1-2^{-24})\times 2^{127}$
最小的正数：$0.100...00\times 2^{00...00}=0.1\times 2^{0-128}=2^{-129}$
因为用原码表示尾数，所以正负对称。
最小的负数：$=-(1-2^{-24})\times 2^{127}$
最大的负数：$=-2^{-129}$

IEEE 754

早起机器，各自定义自己的浮点数形式。机器之间交换数据难，因此规定了一个标准。
以下是一些规定：

阶码：

• 偏置常数：127（单精度），1023（双精度） 这样比128和1024表示的数的范围更大（离0的距离更远）
• 阶码范围：0000 0001（1-127=-126）~ 1111 1110（254-127=127） 全0和全1表示特殊值
• 尾数最高位是1，所以隐含表示，省一位（同上）
• 小数点在1后
• 单精度可表示1+23位，双精度可表示1+52位
  公式
• SP（单精度）$(-1{)}^s\times (1+M)\times 2^{E-127}$
• DP（双精度）$(-1{)}^s\times (1+M)\times 2^{E-1023}$

16进制数转浮点数

BEE0 0000H对应的浮点数是多少呢？
B对应的二进制数是1011
E对应的二进制数是1110
上面的16进制数换成二进制数是1011 1110 1110 0000 0000 0000 0000 0000

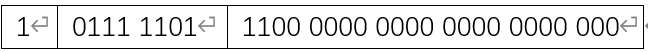
1. 符号位是1，是负数
2. 阶码0111 1101是125，减去127得到-2
3. 尾数0.11+1=1.11=1.75
4. $-1.75\times 2^{-2}=-0.4375$

总结成一个式子就是：
$-1.11\times 2^{01111101-127}=-(2^0+2^{-1}+2^{-2})\times 2^{-2}=-1.75\times 2^{-2}=-0.4375$

浮点数转01序列

$-1.275\times 10^1$

1. $转换成-12.75$
2. $小数点左边12=8+4=1000+0100=1100$
3. $小数点右边0.75=0.5+0.25=0.1+0.01=0.11$
4. 再合起来写成二进制，1100.11
5. $规格化，1.10011\times 2^3$
6. 负数，符号位是1
7. 尾数是110011，省略1就是10011
8. 3加上偏置常数得到阶码是3+127=0000 0011+0111 111=1000 0010
9. 最后得出1 10000010 10011000000000000000000