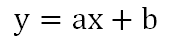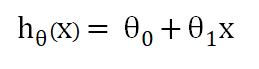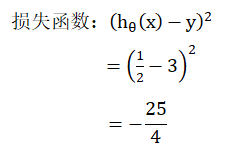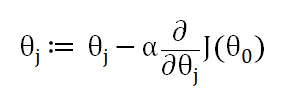saas自助建站/公司推广网站

机器学习可大致分为监督学习和无监督学习、半监督学习几类

其中监督学习主要用在处理分类问题以及回归问题

以下将通过举例监督学习中一个简单的回归问题，来了解机器学习中各种深奥概念

——————————————下面是正文————————————————

一.宏观

       黄金会根据其重量、纯度、加工质量等各种因素从而影响最终的价格，假设我们现在单纯考虑黄金的重量对于价格的影响，那么现在刚好就有一个中国大妈（hiahiahiahia~），她手上刚好有一块前几年在外国便宜入手的黄金打算出手，但是不知道手里的黄金能买多少钱，刚好大妈的广场舞小伙伴收集了该地区各个金铺不同重量的黄金的售价，如图所示：

                                        

                                         PS:上图中星星图标表示随着黄金重量的不同金铺的价格的不同

       对于图中收集而来的众多数据，有个专业名词，叫做 “ 数据集/训练集 ” ！在监督学习中，还有一个名词叫 “ 训练标签 ”，下面会有所涉及。大妈看了这幅图之后，依旧不能正确的推测出自己手上的黄金能买多少钱，因为收集到的黄金重量中没有一个是和自己手上的重量相一致的，怎么办呢？此时，就需要对收集来的数据进行 “ 拟合回归 ”。可以用一条线（线性）来对图上数据进行一个拟合：

                                         

       如此，根据这条直线所示，可以大致推测出大妈手中黄金的价格：

                                         

        对于这种通过数据集来拟合出一条直线从而对新的数据进行预测的过程，既是一个简单完整的人工智能算法，“通过数据集来拟合出一条直线” 这个过程是由电脑自动完成的，专业术语中称之为 “学习/训练过程”，而 “对新的数据进行预测”的过程，是在电脑“学习”完成后，输入新的数据，电脑将返回一个预测的结果，专业术语中称之为 “推理过程”。由此可知，机器学习离不开两个主要的过程：

                                                           学习+推理

       例子是一个单变量（只有黄金重量这个变量）线性（通过一条直线）回归（进行拟合回归）问题，后面还会有多变量线性回归、非线性回归等复杂的机器学习算法，但现在并不涉及。

二.学习过程

       在给定数据集之后，电脑是如何自动进行数据拟合的呢？如本例是个单变量线性回归问题，那么直线可以根据以下线性公式求得：

                                                                           

       在单变量线性回归中，公式会变成这样：

                                                                    

      公式的符号虽然变复杂了，但其实和原来的一模一样，而这个函数就是传说中的 “ 假设函数 ” ，注意：假设函数不是固定唯一的，是根据不同问题会有不同的函数，线性问题一般都是这个。因为 x 为输入进来的数据集，可以假装是固定的：），所以程序只能通过改变另外两个参数进行线性回归，根据参数的不同，最后得出的直线也会不同：

              

       程序怎么知道自己画出来的直线是不是与预测中的直线相同呢？差别很大的话要怎么进行修改呢？这时，“损失函数”和“代价函数” 就显示出它们的重要性了。我们可以用以下图示进行说明：

              

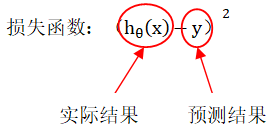
        先抛出“代价函数”和“损失函数” 的公式：

                                                                   

        可以看到，“损失函数” 算出来的是一个数据的结果，而“代价函数” 则是所有数据集结果的总和。但很多时候各大书籍中并没有明确地划分“损失函数” 和 “代价函数” ，一般只用 “代价函数”，甚至有些地方解析为“损失函数” = “代价函数” ，为了理解起来方便，我们在此使用分开的两个概念，再进一步了解公式中每个符号的含义：

                                                                    

       很显然，公式主要是将实际结果和预测结果相减再求平方，变量 y 既是训练集。计算出来的结果怎样才算是最好的呢？可以想象一下，假如实际得到的直线和预测的直线是一致的话，那么放进损失函数计算会得到什么结果呢？是的，由于直线是一致的，那么实际结果和预测结果是一样的，损失函数的结果为零，而“代价函数”不过是将整个数据集的结果相加，形成一个平均值，所以，程序需要做的就是让 “代价函数” 的结果减到最低。

               

      比如图上当黄金重量为 1 时，实际结果算出来的是 1/2，而预测的结果是 3 ，那么投入“损失函数” 来计算就可以得出：

                                                                        

      如果将以上三个数据集都投入“代价函数” 进行计算时，将会得出：

                                                                

       为了让结果降到最低，假设函数的参数应当进行适当调整，令 J 为代价函数的输出结果，根据参数调整的不同，即可以绘出图下所显示的坐标图：

                                                             

       通过不断调整假设函数的参数，可以使代价函数的值降到最低。那么问题来了，程序怎样调整参数才能使得代价函数降到最低呢？使用 “ 梯度下降法 ”。

三.梯度下降法

      话不多说，先抛出梯度下降法的公式：

                                                              

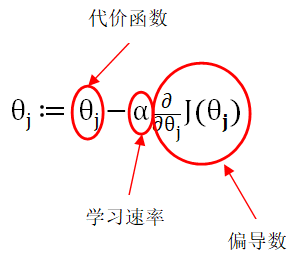
      再对公式进行解析：

                                                                 

      如果看来以上解析还是不了解什么意思的话没关系，我们继续通过例子来理解，我们还是使用 假设函数的参数与代价函数的值J之间的关系图来进行解释：

      如第一次计算时，通过假设函数，再通过代价函数，算出图中星星标志的位置：

                                                      

       由图可知，参数并不是最忧的，所以需要调整，那么根据梯度下降法，可以得出在该点的导数，也就是该点的切线斜率：

                                                       

       该斜率为正，所以公式就可以变为：

                            

       那么往左移动多少呢？这是时候就要看学习速率的了，如果学习速率设置得小，那么相当于跨一个很小的步伐：

                                    

       但是如果学习速率设置得太大的话，那么每一步的跨度将会变大，甚至越过最低点：

                                       

       至于如何设置学习速率才是最合适的，那就要看经验了hiahiahia~而如果第一次计算时，通过假设函数，再通过代价函数，算出图中星星标志的位置：

                                        

        那么根据梯度下降法，可以得出在该点的导数，也就是该点的切线斜率：

                                       

       该斜率为负，所以公式就可以变为：

                                                    

       而后根据学习速率的大小，决定了向右的步伐：

                                 

        但斜率变为 0 时，其值即为最小值：

                                

如此，监督学习中各种常用的概念就基本解释完成了~